石油是国家的经济命脉,稳定的石油供给是经济社会可持续发展的重要保障。2014年我国石油总消耗量为4.9亿吨,其中进口量为2.7亿吨,进口依存度为55%[1]。地下水封石油洞库技术是在地下水位以下岩体中由人工挖掘形成的一定容积洞室中储存各种石油产品的技术。由于具有安全性高、占地面积小、运营成本低等优点,水封储油已成为国内外石油储备的最佳选择与发展方向[2]。地下水封石油洞库的密封性使地下水、岩体和水封系统协同工作得以保证,水封性评价是地下水封石油洞库建设的关键问题。围绕此问题,杨明举等人结合汕头地下水封储气洞库工程,阐述了地下水封洞库储存石油液化气原理,并分析了汕头储气洞库的稳定性和涌水量[3, 4]。李仲奎等人讨论和分析了不衬砌地下洞室在能源储存中的密封措施及关键指标等问题[5]。许建聪等人采用有限差分法研究了地下水封储油洞库涌水量[6]。时洪斌和刘保国依托黄岛地下水封石油洞库,开展了人工水幕水封效果评价,并估算了储油洞室渗流量[7]。蒋中明等人采用 Geoslope 分析了黄岛油库库区地下水位分布特点及变化过程[8]。张振刚等开展了汕头丙烷储库三维渗流场分析,研究了水幕作用及其对储洞周围渗流场的影响[9]。李术才等人开展了基于离散介质流固耦合理论的地下水封石油洞库水封性和稳定性评价[10]。王者超等人采用了多种分析方法,分析了某地下水封石油洞库设计与施工关键技术问题[11, 12, 13, 14, 15, 16, 17]。上述分析多针对洞库整体水封性进行评价,研究对象为库区整体水位和压力分布,但对洞库中相邻洞室之间的水封性研究还不多见。
在节理裂隙岩体渗流模型方面,薛禹群等人分别从地下水动力学和岩土水力学等方面,做了大量系统工作[18, 19, 20, 21, 22]。目前裂隙岩体渗流模型可分为三种基本类型: (1) 等效连续介质渗流模型:把岩体看作等效连续介质体,不考虑裂隙介质的不连续性,如 NEUMAN S P 提出的等效多介质连续体渗流模型[23]; (2) 离散裂隙网络渗流模型:不考虑岩块的渗流,把裂隙作为非连续网络处理,例如 SUDICKY E A 提出的单结构离散裂隙网络渗流模型[24]; (3) 多重介质渗流模型:考虑岩体内裂隙导水、岩块储水等多重效应的裂隙介质模型,例如 CACAS M C 提出基于离散网格分析的连续体渗流模型[25]。
离散裂隙网络模型,把岩体介质系统看作单纯的裂隙介质系统,忽略了岩块中的孔隙系统。离散裂隙网络模型对岩体中的裂隙进行具体的刻画,可以得到裂隙体系中各点真实的渗流状态,具有精度高、拟真性好、计算量小等优点,因此在地下水封石油洞库洞室间水封性评价研究中具有明显优势。本研究介绍了离散裂隙网络法的基本原理和计算过程,针对黄岛地下水封石油洞库,采用离散裂隙网络法进行了7个不同工况的分析,分别获得了水幕压力、洞室间液面差、裂隙倾角和洞室间距对洞库之间水封性的影响。研究成果对地下水封石油洞库的水幕设计及水封性评价具有重要价值。
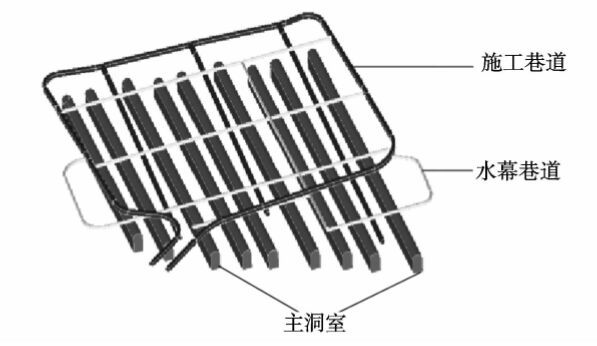
1 工程概况黄岛国家石油储备库地下水封洞库工程是国内首个地下原油储备库建设项目。工程包括地下工程和地上辅助设施两部分,设计地下工程主要包括2条施工巷道、9个主洞室、6条竖井及5条水幕巷道,如图1所示。9个主洞室按南北偏西平行设置,每3个主洞室之间通过4条支洞相连组成一个罐体,共分为3个洞罐组。主洞室设计底板面标高为-50.0 m,长度为500.0~600.0 m不等,设计洞跨20.0 m,洞高30.0 m,截面形状为直墙圆拱形。主洞室顶面以上30.0 m设置5条水幕巷道,垂直主洞室方向布置,总长度约2 835.0 m,设计洞跨为5.0 m,洞高为4.5 m。
|
图1 地下水封石油洞库地下结构图 Fig.1 Underground structures of the underground oil storage caverns |
工程库址区属濒临黄海的低山丘陵区,属低山丘陵地貌。洞库山体为龙雀山,近东西走向,山脊标高为280.0~350.0 m,山脊北侧为陡崖,南侧为陡坡,地形坡度一般为35°~55°,山脊南北两侧发育近南北向及北东向冲沟。洞库主体位于龙雀山南侧,地面平均标高为220.0 m,最高点标高为350.9 m,最低点标高为97.5 m,相对高差为253.4 m。
根据水文地质情况调查,库区地下水以孔隙潜水和裂隙潜水形式赋存。孔隙潜水赋存于表层松散地层中,而裂隙潜水可分为浅层的网状裂隙水和深层的脉状裂隙水。孔隙潜水与浅层网状裂隙水接受大气补给,但由于地势较陡,降水入渗补给地下水量相当少。深层脉状裂隙水主要赋存于断层破碎带内,总体水量较少。库区地下水以山脊作为分水岭,向南北两侧流动。因地下水水力梯度较大,地下水径流较通畅。因此,由于缺少稳定的地下水补给来源,洞库建成后地下水自然补给量十分有限。为确定岩体渗透系数,详细勘查阶段取用了提水及恢复试验、注水消散试验和压水试验进行测试。试验结果表明,该区岩体渗透系数为5.0×10-5~5.0×10-4 m/d,而多数区域岩体渗透系数在1.0×10-4 m/d左右。
2 离散裂隙网络法 2.1 计算原理
离散裂隙网络模型将岩体介质看作由岩体结构面形成的离散裂隙网络。岩体渗透性取决于裂隙网络渗透特性。裂隙网络中,流体流动采用质量守恒定律和立方定律描述。在流体不可压缩条件下,质量守恒方程可表示为
$${{{\rm{d}}{u_x}} \over {{\rm{d}}x}} + {{{\rm{d}}{u_y}} \over {{\rm{d}}y}} + {{{\rm{d}}{u_z}} \over {{\rm{d}}z}} + Q = 0,$$
(1)
将裂隙理想化为二维光滑平行板,在流体为定常流条件下,并忽略惯性力影响,流体流动的控制方程可采用立方定律描述。立方定律可表示为
$$q = - {{\rho g{e^3}} \over {12\mu }} \cdot {{{\rm{d}}h} \over {{\rm{d}}x}},$$
(2)
设离散裂隙网络中任一节点i处有m条裂隙与其相连,则根据质量守恒有
$$(\sum\limits_{j = 1}^m {{q_j}} ) + {Q_i} = 0,(i = 1,2,3, \cdot \cdot \cdot ,n),$$
(3)
将裂隙网络所有节点质量守恒方程联立,结合边界条件,即可获得问题求解的线性方程组。求解线性方程组则可以得到各节点的水头,再根据式(2)即可计算各条裂隙上流体的流速。
2.2 计算步骤离散裂隙网络法主要计算步骤如下:
第1步,根据地质条件划分裂隙网络,对节点和裂隙编号;
第2步,根据问题特征,设置边界条件;
第3步,对裂隙网络中每个节点列出质量守恒方程,并利用立方定律将与其连通的裂隙流量带入,获得节点处求解方程;
第4步,将所有节点方程联立,获得问题求解的方程组
[A]n×n[h]n×1=[b]n×1,
(4)
第5步,求解式(2),得到各个节点的总水头和各条裂隙的流速;
第6步,对计算结果进行处理,绘制等水头图和流速矢量图。
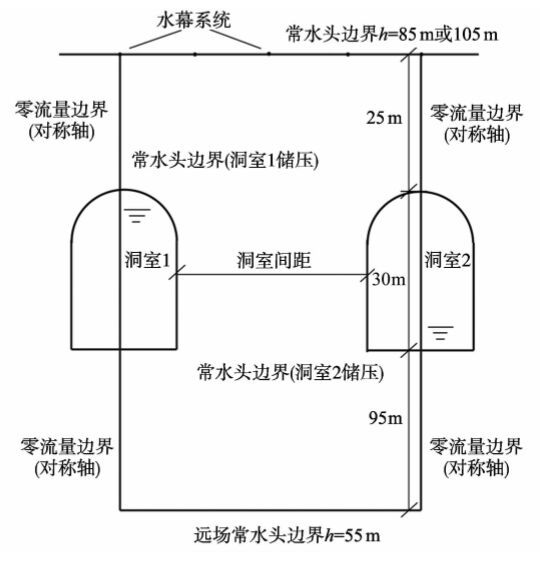
3 地下石油洞库水封性评价方法 3.1 评价模型根据黄岛地下水封石油洞库的工程情况,水封性评价模型如图2所示。储油洞室为马蹄形,宽20 m,高30 m。洞室间距为30、40、50 m不等。研究范围如下:上方至水幕巷道,高度为拱顶上方25 m;下方取洞室底板以下95 m;左右两侧则根据对称性取相邻洞室的轴线。选取洞室底板处位置水头为0 m。边界条件设置如下:根据对称性,对称轴上流量为0;上边界水幕系统为常水头边界,其值取决于施加水幕压力;下边界取在洞室影响范围之外,为常水头,其值为55 m;两个洞室洞壁水头则由储油压力决定。根据地质勘查资料,研究范围内岩体中发育有两组裂隙,且裂隙隙宽相同。
|
图2 地下水封石油洞库洞室间水封性评价示意图 Fig.2 Illustration of the inter-cavern containment assessment for underground oil storage caverns |
根据上述讨论,影响相邻洞室间水封性的因素主要有:(1)相邻洞室间液面差;(2)水幕系统压力;(3)相邻洞室间距;(4)裂隙倾角。为了研究上述因素对水封性影响,设计了如表1所示7个工况。
| 表1 模拟工况 Table 1 The simulated conditions |
工况1为代表性工况,该工况中相邻洞室间液面差为20 m,水幕系统水头85 m,洞室间距为30 m,裂隙倾角为15°和75°;
工况2中,相邻洞室间液面差为10 m,其他条件与工况1相同;
工况3中,水幕系统水头为105 m,其他条件与工况1相同;
工况4和5中,洞室间距分别为40 m和50 m,其他条件与工况1相同;
工况6和7中,裂隙倾角分别为54°、106°和84°、136°,其他条件与工况1相同。
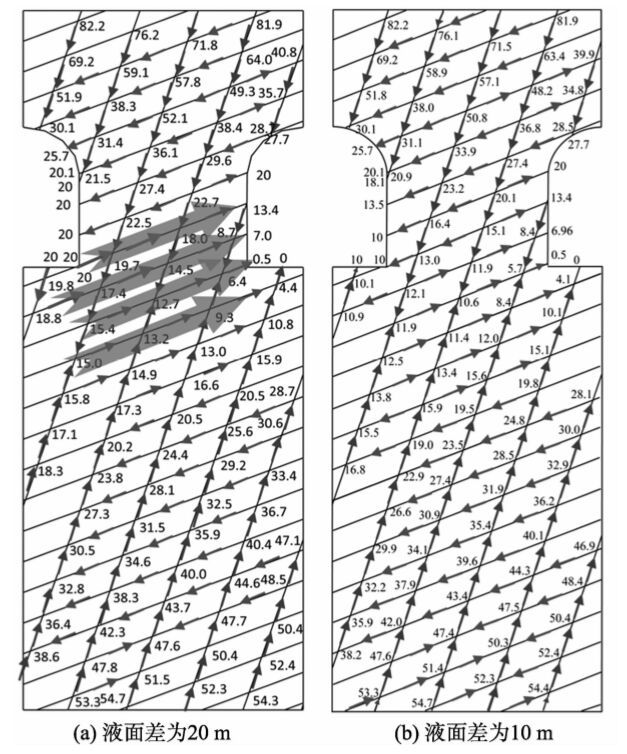
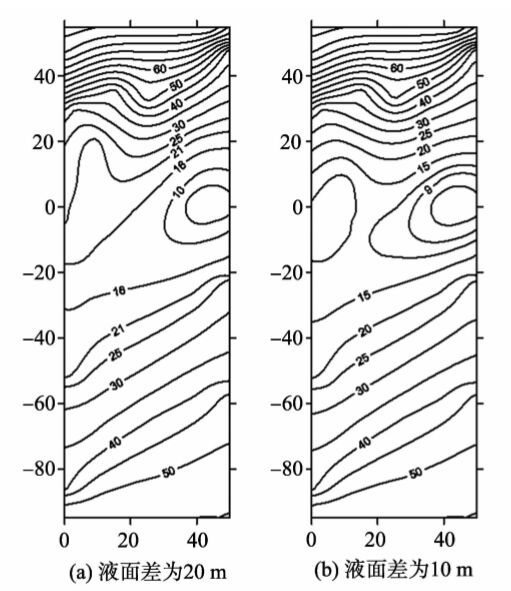
4 评价结果 4.1 洞室间液面差影响图3(a)和图3(b)分别为工况1和工况2条件下研究范围内裂隙网络节点处水头和裂隙内水的流动矢量方向分布图。图4(a)和图4(b)分别为工况1和工况2条件下研究范围内等水头线分布图。整体看,由于洞室开挖,洞室周围为研究范围内水头较低的区域,而水幕系统和研究区域下方岩体中地下水补给到洞室周围岩体。
|
图3 工况1和工况2中水头分布和流动矢量方向 Fig.3 Water head distribution and flow vector direction in case 1 and case 2 |
|
图4 工况1和工况2地下水等水头线分布图 Fig.4 Isograms of underground water head in case 1 and case 2 |
工况1中,相邻洞室间液面差为20 m,在此条件下,相邻洞室间岩柱下端出现了4条渗漏裂隙,沿渗漏裂隙地下水水头逐渐降低。而工况2中液面差为10 m,在此条件下,上方水幕系统的水沿岩柱向左右两侧洞室渗透,岩柱中并未出现渗漏现象。由于流体流动方向与等势线垂直,因此工况1中将会出现由左侧洞室到右侧洞室的流线,而工况2则不会出现。因此,减少相邻洞室间液面差可以提高洞室间水封性。
4.2 水幕压力影响图5(a)为工况3条件下研究范围内裂隙网络节点处水头和裂隙内流动矢量方向分布图。图5(b)为工况3地下水等水头线分布图。与工况1计算结果对比,水幕系统水头增加20 m条件下,相邻洞室间水头略有增加,但仍然存在渗漏现象。这可能是由于水幕系统水头增加,引起了岩柱上端水头较大程度增加,但是由于岩柱较为狭窄,对岩柱下端影响有限。因此,在洞室间距较小条件下,仅靠增加水幕压力并不能保证洞室间水封性。
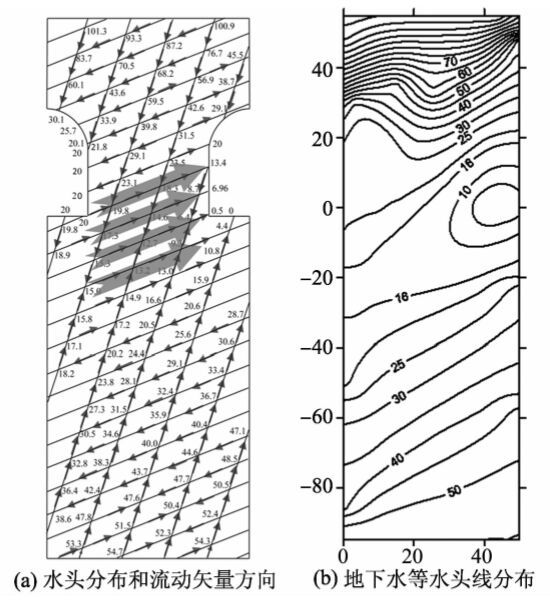
|
注:宽箭头表示渗漏路径。 图5 工况3中水头分布、流动矢量方向和地下水等水头线分布图 Fig.5 Water head distribution,flow vector direction and isogram of underground water head in case 3 |
图6(a)和图6(b)分别为工况4和工况5条件下研究范围内裂隙网络节点处水头和裂隙内流动矢量方向分布图。图7(a)和图7(b)分别为两个工况条件下研究范围内等水头线分布图。与工况1计算结果对比,当洞室间距为30 m和40 m时,相邻洞室间存在渗漏现象,但当洞室间距增加到50 m时,相邻洞室不再出现渗漏现象。因此,增加洞室间距,可以使得水幕系统的水封性更好。这可能是由于在裂隙间距保持不变条件下,增加洞室间距会增加竖向裂隙数,使得水幕系统和远场地下水可以补给到洞室岩柱处。
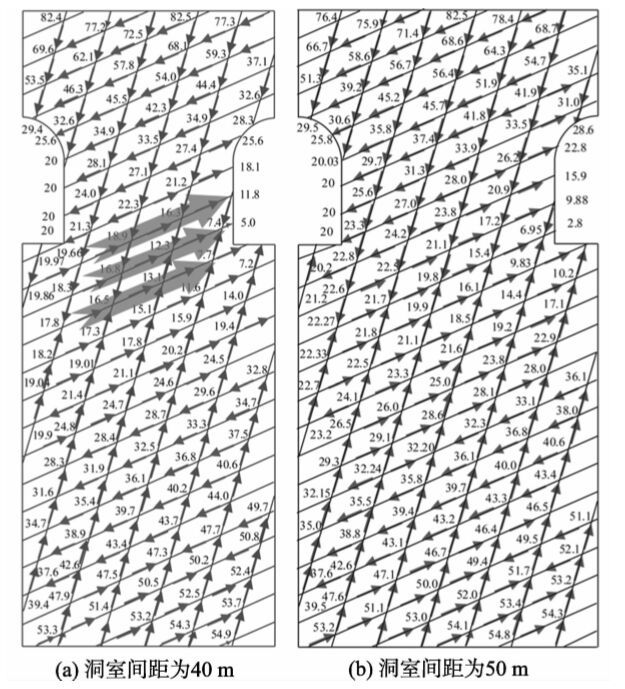
|
注:宽箭头表示渗漏路径 图6 工况4和工况5中水头分布和流动矢量方向 Fig.6 Water head distribution and flow vector direction in case 4 and case 5 |
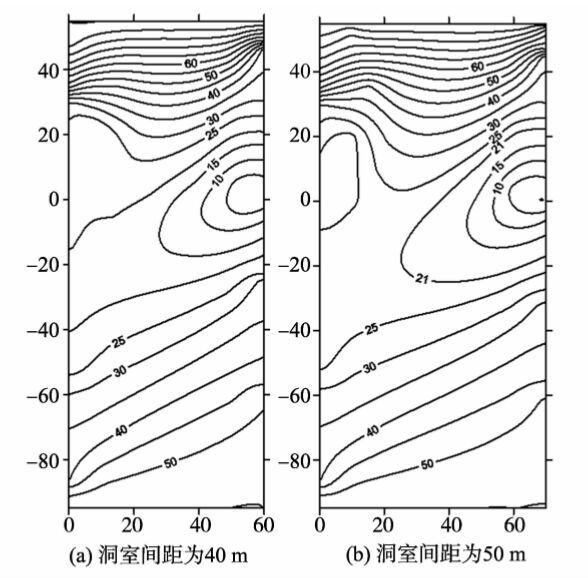
|
图7 工况4和5地下水等水头线分布图 Fig.7 Isograms of underground water head in case 4 and case 5 |
图8(a)和图8(b)分别为工况6和工况7条件下研究范围内裂隙网络节点处水头和裂隙内流动矢量方向分布图,图9(a)和图9(b)为两个工况条件下研究范围内等水头线分布图。工况6和7中,裂隙倾角分别为54°、106°和84°、136°,从图8(a)和图8(b)中看,在两个工况条件下,相邻洞室均未出现渗漏现象。
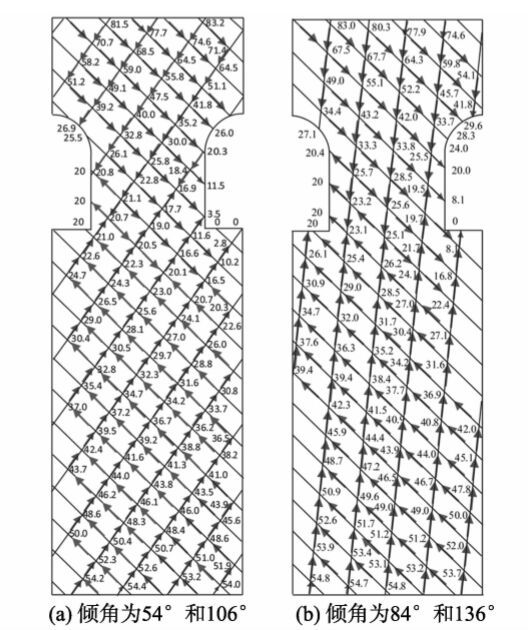
|
图8 工况6和工况7中水头分布和流动矢量方向 Fig.8 Water head distribution and flow vector direction in case 6 and case 7 |

|
图9 工况6和7地下水等水头线分布图 Fig.9 Isograms of underground water head in case 6 and case 7 |
分析原因如下:设裂隙隙宽为0.01 mm,采用渗透系数张量计算公式,计算工况1、6和7中岩体渗透张量最大和最小渗透系数主值和主方向。渗透张量计算公式为[26]
\[K=\sum\limits_{i=1}^{m}{\frac{\rho ge_{i}^{3}}{12\mu {{s}_{i}}}}\left[ \begin{matrix}
{{K}_{xxi}} & {{K}_{xyi}} & {{K}_{xzi}} \\
{{K}_{yxi}} & {{K}_{yyi}} & {{K}_{yzi}} \\
{{K}_{zxi}} & {{K}_{zyi}} & {{K}_{zzi}} \\
\end{matrix} \right],\]
(5)
Kxxi=1-sin2αicos2βi;
Kxyi=Kyxi=-sin2αi cosβisinβi;
Kzyi=Kyzi=-sinαicosαicosβi;
Kyyi=1-sin2αisin2 βi;
Kzyi=Kyzi=-sinαicosαisinβi; Kzzi=sin2αi;
ρ为液体密度;μ为液体动力粘滞系数取8.39×10-4;g为重力加速度;si为裂隙间距。计算结果列于表2,由表2可知,工况1中优势渗流路径方向更接近于水平方向,而工况6和7则更接近竖直方向,因此工况6和7中裂隙分布能为洞库提供更好的水封条件。| 表2 工况1,工况6和工况7岩体渗透张量主值及其方向 Table 2 Principal values of the permeability tensor of rock mass and its direction in case 1,case 6 and case 7 |
上述7个工况中,工况1、工况3、工况6出现了渗漏现象,假设裂隙隙宽为0.01 mm,洞室长度为500 m,采用式(2)对各个工况渗漏量进行估算,可得3种工况条件下渗漏量分别为0.124、0.126和0.075 m3/d。
5 结论本研究以中国首个大型水封地下石油洞库为背景,采用离散裂隙网络法开展了地下水封石油洞库相邻洞室间水封性评价研究。介绍了离散裂隙网络法的计算原理,提出了计算方法;采用离散裂隙网络法,开展了黄岛地下石油洞库水封性的评价研究,获得了不同因素对洞库水封性的影响特征。研究结果表明:(1) 水幕压力增大,洞室间液面差减小,洞室间距增大,均会使洞库水封性得到改善;(2) 裂隙倾角的变化会影响裂隙网络中优势渗流路径,从而影响地下石油洞库的水封性;(3) 地下水封石油洞库相邻洞室水封设计应综合考虑储油情况、洞室间距、裂隙倾角等因素,而单纯增加水幕系统压力并不能保证洞室间水封性。本研究仅考虑了两组贯通等间距裂隙对洞室间水封性的影响,而工程岩体中裂隙发育规律较为复杂,因此将来有必要开展复杂裂隙条件下洞室间水封性评价研究。
| [1] | 田春荣. 2014年中国石油和天然气进出口状况分析[J]. 国际石油经济, 2015, 23(3):57-67. TIAN Chunrong. Analyses of import and export situation of China national petroleum and natural gas in 2014[J]. International Petroleum Economics, 2015, 23(3):57-67.(  1) 1) |
| [2] | 王梦恕, 杨森. 地下水封岩洞油库是储存油品的最好型式[C]//中国土木工程学会第十一届、隧道及地下工程分会第十三届年会论文集增刊. 北京: 中国工程科学, 2004. WANG Mengshu, YANG Sen. Underground cave oil depot is the best type of oil storage[C]//Chinese Civil Engineering Society Eleventh, Tunnel and Underground Engineering of the Thirteenth Annual Meeting Proceedings Supplement. Beijing:Engineering Sciences, 2004.(  1) 1) |
| [3] | 杨明举, 关宝树. 地下水封储气洞库原理及数值模拟分析[J]. 岩石力学与工程学报, 2001, 20(3):301-305. YANG Mingju, GUAN Baoshu. Simulation analysis of underground gas storage caverns and numerical principle[J]. Chinese Journal of Rock Mechanics and Engineering, 2001, 20(3):301-305.(  1) 1) |
| [4] | 杨明举, 关宝树. 地下水封裸洞储存LPG耦合问题的变分原理及应用[J]. 岩石力学与工程学报, 2003, 22(4):515-520. YANG Mingju, GUAN Baoshu. Variational principle and application of LPG coupling problem in groundwater sealing and bare hole storage[J]. Chinese Journal of Rock Mechanics and Engineering, 2003, 22(4):515-520.(  1) 1) |
| [5] | 李仲奎, 刘辉, 曾利, 等. 不衬砌地下洞室在能源储存中的作用与问题[J]. 地下空间与工程学报, 2005, 1(3):350-357. LI Zhongkui, LIU Hui, ZENG Li, et al. Effect of unlined underground caverns in energy storage and some related problems[J]. Chinese Journal of Underground Space and Engineering, 2005, 1(3):350-357.(  1) 1) |
| [6] | 许建聪, 郭书太. 地下水封油库围岩地下水渗流量计算[J]. 岩土力学, 2010, 31(4):1295-1302. XU Jiancong, GUO Shutai. Seepage discharge calculation of surrounding rock groundwater in rock caverns sealed oil storage[J]. Rock and Soil Mechanics, 2010, 31(4):1295-1302.(  1) 1) |
| [7] | 时洪斌, 刘保国. 水封式地下储油洞库人工水幕设计及渗流量分析[J]. 岩土工程学报, 2010, 32(1):130-137. SHI Hongbin, LIU Baoguo. Design and seepage discharge analysis of artificial water curtains for water sealed underground petroleum storage caverns in rock[J]. Chinese Journal of Geotechnical Engineering, 2010, 32(1):130-137.(  1) 1) |
| [8] | 蒋中明, 冯树荣, 曹铃, 等. 水封油库地下水位动态变化特性数值模拟[J]. 岩土工程学报, 2011, 33(11):1780-1785. JIANG Zhongming, FENG Shurong, CAO Ling, et al. Numerical study on variation features of water table in area of underground rock cavern for oil storage[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(11):1780-1785.(  1) 1) |
| [9] | 张振刚, 谭忠盛, 万姜林, 等. 水封式LPG地下储库渗流场三维分析[J]. 岩土工程学报, 2003, 25(3):331-335. ZHANG Zhengang, TAN Zhongsheng, WAN Jianglin, et al. Three-dimensional seepage analysis of underground LPG storage with water curtain[J]. Chinese Journal of Geotechnical Engineering, 2003, 25(3):331-335.(  1) 1) |
| [10] | 李术才, 平洋, 王者超, 等. 基于离散介质流固耦合理论的地下石油洞库水封性和稳定性评价[J]. 岩石力学与工程学报, 2012, 31(11):1-11. LI Shucai, PING Yang, WANG Zhechao, et al. Assement of containment and stablity of underground crude oil storage caverns based on fluid-solid coupling theory for discrete medium[J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(11):1-11.(  1) 1) |
| [11] | 王者超, 李术才, 乔丽苹, 等. 大型地下石油洞库自然水封性应力渗流耦合分析[J]. 岩土工程学报, 2013, 35(8):1535-1543. WANG Zhechao, LI Shucai, QIAO Liping, et al. Assessment of natural containment property of an underground crude oil storage caverns using fluid flow-stress coupling method[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(8):1535-1543.(  1) 1) |
| [12] | 王者超, 李术才, 薛翊国, 等. 大型地下水封石油洞库围岩完整性、变形和稳定性分析[J]. 山东大学学报(工学版), 2011, 41(3):112-118. WANG Zhechao, LI Shucai, XUE Yiguo, et al. Integrity, deformation and stability of a rock mass around underground crude oil storage caverns in containment of groundwater[J]. Journal of Shandong University(Engineering Science), 2011, 41(3):112-118.(  1) 1) |
| [13] | 梁建毅, 李术才, 薛翊国, 等. 地下储油库岩体水文地质分类及工程应用研究[J]. 山东大学学报(工学版), 2012, 42(6):112-118. LIANG Jianyi, LI Shucai, XUE Yiguo, et al. Rock mass classfication for underground facility with emphasis on hydrogeology and its engineering application[J]. Journal of Shandong University (Engineering Science), 2012, 42(6):112-118.(  1) 1) |
| [14] | 王者超, 李术才, 薛翊国, 等. 大型地下水封石油洞库施工过程力学特性研究[J]. 岩土力学, 2013, 34(1):275-282. WANG Zhechao, LI Shucai, XUE Yiguo, et al. Mechanical properties of surrounding rocks of large water sealed underground oil storage caverns during construction process[J]. Rock and Soil Mechanics, 2013, 34(1):275-282.(  1) 1) |
| [15] | 王者超, 李术才, 梁建毅, 等. 地下水封石油洞库渗水量预测与统计[J]. 岩土工程学报, 2014, 36(8):1490-1497. WANG Zhechao, LI Shucai, LIANG Jianyi, et al. Prediction and measurement of groundwater flow rate of underground crude oil storage caverns[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(8):1490-1497.(  1) 1) |
| [16] | 王者超, 李术才, 薛翊国, 等. 地下水封石油洞库水幕系统设计原则与连通性判断方法研究[J]. 岩石力学与工程学报, 2014, 33(2):276-286. WANG Zhechao, LI Shucai, XUE Yiguo, et al. Design principles and inter-connectivity determination method of groundwater curtaining system for underground crude oil storage caverns[J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 33(2):276-286.(  1) 1) |
| [17] | 平洋,王者超,李术才,等. 裂隙随机分布条件下地下石油洞库水封性评价[J]. 岩土力学, 2014, 35(3): 811-819. PING Yang, WANG Zhechao, LI Shucai, et al. Water seal effect evaluation of underground crude oil storage caverns around rock mass with random joints[J]. Rock and Soil Mechanics, 2014, 35(3):811-819.(  1) 1) |
| [18] | 薛禹群. 地下水动力学[M]. 2版. 北京: 地质出版社, 2003.( 1) 1) |
| [19] | 周创兵, 陈益峰, 姜清辉, 等. 复杂岩体多场广义耦合分析导论[M]. 北京: 中国水利水电出版社, 2008.( 1) 1) |
| [20] | 仵彦卿. 岩土水力学[M]. 北京: 科学出版社, 2009.( 1) 1) |
| [21] | 周志芳. 裂隙介质水动力学原理[M]. 北京: 高等教育出版社, 2007.( 1) 1) |
| [22] | 朱珍德, 郭海庆. 裂隙岩体水力学基础[M]. 北京: 科学出版社, 2007.( 1) 1) |
| [23] | NEUMAN S P, DEPNER J S. Use of variable-scale pressure test data to estimate the log hydraulic conductivity covariance and dispersivity of fractured granites near Oracle[J]. Journal Hydrology, 1988, 10(2):475-501.( 1) 1) |
| [24] | SUDICKY E A, MCLAREN R G. The Laplace Transform Galerkin technique for large-scale simulation of mass transport in discretely fractured porous formations[J]. Water Resources Research, 1992, 28(2): 499-514.( 1) 1) |
| [25] | CACAS M C, LEDOUX E, DEMARSILY G, et al. Modeling fracture flow with a stochastic discrete fracture network: calibration and validation[J]. Water Resources Research, 1990, 26(3):479-489.( 1) 1) |
| [26] | 王媛, 徐志英, 速宝玉, 等. 复杂裂隙岩体渗流与应力弹塑性全耦合分析[J].岩石力学与工程学报, 2000, 19(2):177-181. WANG Yuan, XU Zhiying, SU Baoyu, et al. Complete coupled analysis of fluid flow and elastoplastic stress in complicated fractured rock masses[J]. Chinese Journal of Rock Mechanics and Engineering, 2000, 19(2):177-181.(  1) 1) |



