0 引言

随着随机微分方程理论的发展,尤其是It K提出It公式以来,越来越多的随机系统模型成功应用于科学领域以及工程实际中。许多确定性系统中的概念和问题推广到随机系统,如稳定性概念、能观测(检测)性概念、线性二次问题等。另一方面,Markov跳跃系统因能描述大量实际系统而广受关注,许多研究成果应运而生。在此基础上,两者结合的随机Markov跳跃系统的研究工作也逐渐展开。文献^[1]首次系统地介绍了随机Markov跳跃系统的各种稳定性,包括指数稳定、δ阶矩稳定、几乎处处稳定、依概率稳定等,并讨论了其在金融、人口动力学及控制上的一些应用。文献^{[2, 3]}给出了扩散项不含控制时随机Markov跳跃系统几乎处处指数能稳的充分条件和随机Markov跳跃延迟系统的鲁棒稳定性及能控性条件。文献^[4]则考虑了随机It跳跃系统的鲁棒滤波问题。针对随机离散Markov跳跃系统,文献^[5]应用Riccati方程方法研究了系统的稳定性。以上关于稳定性的研究大多关注的是系统在无限时域内的渐近行为。然而,在工业实际中,一个稳定的系统可能具有较坏的暂态性能(如振荡剧烈),从而影响生产过程。为了解决这类问题,人们开始关心系统在有限时间上的稳定性,文献^[6]首次提出了确定性系统短时间稳定的概念。以此为基础,文献^[7]提出了系统有限时间有界的概念。文献^[8]讨论了系统的有限时间镇定问题,即寻找一个反馈控制器使闭环系统有限时间稳定。文献^[9]考虑了离散系统的有限时间镇定问题,通过线性矩阵不等式(linear matrix inequality,LMI)方法设计了反馈增益矩阵。实际系统中的有限时间控制问题也受到了关注,例如航天器姿态跟踪系统^[10]、可重复使用运载器^[11]。文献^[12]首次对随机It系统提出了有限时间随机鲁棒稳定的概念,并给出了系统稳定以及镇定的充分条件。文献^{[13, 14]}分别讨论了两类不同随机系统的有限时间静态和动态输出反馈控制。文献^[15]则研究了随机线性It系统的有限时间保成本控制问题。然而,目前针对随机Markov跳跃系统的有关研究还较少。

本文在前人工作的基础上给出了连续时间随机Markov跳跃系统的有限时间随机稳定和有限时间有界的概念,利用Lyapunov和LMI方法得到了系统稳定以及能稳的条件,并进行了能稳控制器设计。

1 系统描述

连续时间随机Markov跳跃系统

$\left\{ \begin{matrix} dx\left( t \right)=A\left( r \right)x\left( t \right)dt+C\left( {{r}_{t}} \right)x\left( t \right)dw, \\ x\left( 0 \right)={{x}_{0}}\in {{R}^{n}}, \\ \end{matrix} \right.$

(1)

所对应的受控系统为

$\left\{ \begin{matrix} dx\left( t \right)=\left[ A\left( {{r}_{t}} \right)x\left( t \right)+B\left( {{r}_{t}} \right)u\left( t \right) \right]dt+\left[ C\left( {{r}_{t}} \right)x\left( t \right)+D\left( {{r}_{t}} \right)u\left( t \right) \right]dw\left( t \right), \\ x\left( 0 \right)={{x}_{0}}\in {{R}^{n}}, \\ \end{matrix} \right.$

(2)

式中:x(t)∈Rⁿ为系统状态向量;u(t)∈R^m为控制输入; x₀∈Rⁿ为系统初始状态;A(r_t)、B(r_t)、C(r_t)、D(r_t)为适当维数的矩阵;w(t)是定义在滤波概率空间(Ω,F,P)上的一维标准Wiener过程,w(0)=0;跳跃过程｛r_t,t≥0｝为连续时间齐次Markov链,其状态空间为S=｛1,2,…,l｝,w(t)与｛r_t,t≥0｝相互独立。转移概率

$P\left( {{r}_{t+h}}=j|{{r}_{t}}=i \right)=\left\{ \begin{matrix} {{q}_{ij}}h+o\left( h \right),i\ne j, \\ 1+{{q}_{ij}}h+o\left( h \right),i=j, \\ \end{matrix} \right.$

式中: h为时间增量,h>0,$\underset{h\to 0}{\mathop{\lim }}\,\frac{o\left( h \right)}{h}$=0。当i≠j时,q_ij≥0,表示由t时刻模态i转移到t+h时刻模态j的概率;当i=j时,q_ii=-$\sum\limits_{j\in S,j\ne i}^{{}}{{}}$q_ij≤0即$\sum\limits_{j=1}^{l}{{}}$q_ij=0。转移概率矩阵

$\Lambda =\left[ \begin{matrix} {{q}_{11}} & {{q}_{12}} & \cdots & {{q}_{1l}} \\ {{q}_{21}} & {{q}_{22}} & \cdots & {{q}_{2l}} \\ \vdots & \vdots & \ddots & \vdots \\ {{q}_{l1}} & {{q}_{l2}} & \cdots & {{q}_{ll}} \\ \end{matrix} \right]。$

2 有限时间随机稳定

定义 1  系统(1)称为关于(c₁,c₂,T,R_i)有限时间随机稳定的,如果

$E\left( x_{0}^{T}{{R}_{i}}{{x}_{0}} \right)\le {{c}_{1}}\Rightarrow E\left[ {{x}^{T}}\left( t \right){{R}_{i}}x\left( t \right) \right]<{{c}_{2}},\forall t\in \left[ 0,T \right],$

式中: c₁,c₂ 为给定常数,c₂>c₁>0; R_i为给定的方阵,且R_i>0(i∈S)。系统(2)称为有限时间随机能稳的,如果存在反馈控制 u(t)=$\sum\limits_{i=1}^{l}{{}}$K_ix(t)I_｛rt=i｝,使闭环系统

$\left\{ \begin{matrix} dx\left( t \right)=\left[ A\left( {{r}_{t}} \right)+B\left( {{r}_{t}} \right)K\left( {{r}_{t}} \right) \right]x\left( t \right)dt+\left[ C\left( {{r}_{t}} \right)+D\left( {{r}_{t}} \right)K\left( {{r}_{t}} \right) \right]x\left( t \right)dw\left( t \right), \\ x\left( 0 \right)={{x}_{0}}\in {{R}^{n}}, \\ \end{matrix} \right.$

是有限时间随机稳定的。这里,K_i为适当维数的矩阵,I_｛·｝为示性函数。

注 1  有限时间随机(finite-time stochastic,FTS)稳定与均方稳定是两个独立的概念,不存在包含关系。FTS稳定性描述的是系统在有限时间间隔上的某种暂态性能,即给定有限的初始状态,系统在特定时间内的状态不超过某个界。因此,定义中R_i>0(i∈S)可以换成R>0,不影响它的含义。

首先,给出系统FTS稳定的充分必要条件。

定理 1  系统(1)关于(c₁,c₂,T,R_i)FTS稳定的充分必要条件是:

$E\left( x_{0}^{T}{{R}_{i}}{{x}_{0}} \right)\le {{c}_{1}}\Rightarrow Tr\left[ {{R}_{i}}{{Q}_{i}}\left( t \right) \right]<{{c}_{2}},\forall t\in \left[ 0,T \right],$

式中矩阵Q_i(t)(i∈S)为方程

$\left\{ \begin{matrix} {{{\dot{Q}}}_{i}}\left( t \right)={{A}_{i}}{{Q}_{i}}\left( t \right)+{{Q}_{i}}\left( t \right)A_{i}^{T}+{{C}_{i}}{{Q}_{i}}\left( t \right)C_{i}^{T}+\sum\limits_{i=1}^{l}{{{q}_{ji}}{{Q}_{j}}} \\ {{Q}_{i}}\left( 0 \right)=E\left( {{x}_{0}}x_{0}^{T}{{I}_{\left\{ {{r}_{0}}=i \right\}}} \right) \\ \end{matrix} \right.$

(3)

的解。

证明  令Q_i(t)=E[x(t)x^T(t)I_｛rt=i｝]。由文献^[16]定理2.1知Q_i(t)为式(3)的解,而E[x^T(t)R_ix(t)]=ETr[R_ix(t)x^T(t)]=Tr[R_iQ_i(t)]。证毕。

这里虽然给出了系统FTS稳定的充要条件,但是验证起来比较困难,下面给出系统FTS稳定的充分条件,可以利用LMI方法来判断。

引理 1^[17]  假设v(t)为[0,T]上的非负函数,使得v(t)≤C+A$\int{_{0}^{t}}$v(s)ds(0≤t≤T),其中C、A为常数,则v(t)≤Ce^At,0≤t≤T。

定理 2  (ⅰ) 如果对于某个α≥0,存在正定矩阵Q_i(i∈ S)使得

$A_{i}^{T}{{Q}_{i}}+{{Q}_{i}}{{A}_{i}}+C_{i}^{T}{{Q}_{i}}{{C}_{i}}-\alpha {{Q}_{i}}+\sum\limits_{j=1}^{l}{{{q}_{ji}}}{{Q}_{j}}<0$

(4)

$\frac{{{c}_{1}}}{{{c}_{2}}}$eαTI<${{{\bar{Q}}}_{i}}$

(5)

成立,则系统(1)FTS稳定。式中${{{\bar{Q}}}_{i}}$=$R_{i}^{-\frac{1}{2}}$Q_i$R_{i}^{-\frac{1}{2}}$,I为单位矩阵。

(ⅱ) 如果对于某个α≥0,存在矩阵P_i>0以及Y_i(i∈S)使得

$\left[ \begin{array}{*{35}{l}} {{\Phi }_{i}}-\alpha {{P}_{i}}+{{q}_{ii}}{{P}_{i}} & {{P}_{i}}C_{i}^{T}+Y_{i}^{T}D_{i}^{T} & {{\Psi }_{i}} \\ * & -{{P}_{i}} & 0 \\ * & * & -{{\Theta }_{i}} \\ \end{array} \right]<0,$

(6)

I<${{{\bar{P}}}_{i}}<\frac{{{c}_{1}}}{{{c}_{2}}}{{e}^{-\alpha T}}I,$

(7)

成立,则系统(2)FTS能稳,且u(t)=$\sum\limits_{i=1}^{l}{{}}$K_ix(t)I_｛rt=i｝=$\sum\limits_{i=1}^{l}{{}}$Y_iP_i^-1x(t)I_｛rt=i｝为能稳控制。式中:Φ_i=P_iA_i^T+A_iP_i+B_iY_i+Y_i^TB_i^T; ψ_i=($\sqrt{{{q}_{il}}}$P₁,…,$\sqrt{{{q}_{il-1}}}$P_i-1,$\sqrt{{{q}_{il+1}}}$P_i+1,…,$\sqrt{{{q}_{il}}}$P_l); Θ_i=diag(P₁,…,P_i-1,P_i+1,…,P_l);${{{\bar{P}}}_{i}}$=$R_{i}^{\frac{1}{2}}{{P}_{i}}R_{i}^{\frac{1}{2}}$;*表示对称矩阵的对称部分。

证明  (ⅰ) 取随机Lyapunov算子V(x,i)=x^TQ_ix(i∈S),式(1)的无穷小生成元

$LV\left( x,i \right)={{x}^{T}}\left( A_{i}^{T}{{Q}_{i}}+{{Q}_{i}}{{A}_{i}}+C_{i}^{T}{{Q}_{i}}{{C}_{i}} \right)x+\sum\limits_{j=1}^{l}{{{q}_{ji}}{{x}^{T}}{{Q}_{j}}}x,$

显然,式(4)等价于LV(x,i)<αV(x,i),两端从0到t(t∈[0,T])积分,并取期望,得

EV(x,i)<V(x0,i)+α$\int{_{0}^{t}}$V(x(s),i)ds。

由引理1,EV(x,i)<V(x₀,i)e^αt,而EV(x,i)=E( x^TQ_ix)=E(${{x}^{T}}R_{i}^{\frac{1}{2}}{{{\bar{Q}}}_{i}}R_{i}^{\frac{1}{2}}x$)≥λ_min(${{{\bar{Q}}}_{i}}$)E(x^TR_ix),V(x₀,i)e^αt=E(x₀^TQ_ix₀)e^αt=E($x_{0}^{T}R_{i}^{\frac{1}{2}}{{{\bar{Q}}}_{i}}R_{i}^{\frac{1}{2}}{{x}_{0}}$)e^αt≤λ_max(${{{\bar{Q}}}_{i}}$)x₀^TR_ix₀e^αt≤λ_max(${{{\bar{Q}}}_{i}}$)c₁e^αT,所以,E(x^TR_ix)≤$\frac{{{\lambda }_{\max }}\left( {{{\bar{Q}}}_{i}} \right)}{{{\lambda }_{\min }}\left( {{{\bar{Q}}}_{i}} \right)}$c₁e^αT=cond(${{{\bar{Q}}}_{i}}$)c₁e^αT。易得,当式(5)成立时,E(x^TR_ix)<c₂。

(ⅱ) 将式(4)中的A_i换成A_i+B_iK_i,C_i换成C_i+D_iK_i,并令P_i=Q_i^-1,Y_i=K_iP_i,通过恒等变形以及Schur补即得式(6)、(7),由式(5)以及P_i、Q_i、${{{\bar{Q}}}_{i}}$之间的关系可得。证毕。

3 有限时间有界

考虑如下系统

$\left\{ \begin{matrix} dx\left( t \right)=\left[ A\left( {{r}_{t}} \right)x\left( t \right)+B\left( {{r}_{t}} \right)u\left( t \right)+G\left( {{r}_{t}} \right)v\left( t \right) \right]dt+\left[ C\left( {{r}_{t}} \right)x\left( t \right)+H\left( {{r}_{t}} \right)v\left( t \right) \right]dw\left( t \right), \\ x\left( 0 \right)={{x}_{0}}\in {{R}^{n}}, \\ \end{matrix} \right.$

(8)

以及受控系统

$\left\{ \begin{matrix} \begin{align} & dx\left( t \right)=\left[ A\left( {{r}_{t}} \right)x\left( t \right)+B\left( {{r}_{t}} \right)u\left( t \right)+G\left( {{r}_{t}} \right)v\left( t \right) \right]dt+ \\ & \left[ C\left( {{r}_{t}} \right)x\left( t \right)+D\left( {{r}_{t}} \right)u\left( t \right)+H\left( {{r}_{t}} \right)v\left( t \right) \right]dw\left( t \right), \\ \end{align} \\ x\left( 0 \right)={{x}_{0}}\in {{R}^{n}}, \\ \end{matrix} \right.$

(9)

式中: v(t)∈R^k为外部干扰;G(r_t)、H(r_t)为适当维数的矩阵。

首先,给出系统有限时间有界(finite-time boundedness,FTB)的概念。

定义 2  系统(8)称为关于(c₁,c₂,T,R_i,d)有限时间有界,如果E(x₀^TQ_ix₀)≤c₁$\Rightarrow $E[x^T(t)R_ix(t)]<c₂,$\forall $t∈[0,T],这里,v(t):$\int{_{0}^{T}}$v^T(t)v(t)dt≤d,c₂>c₁>0,T>0,d≥0为给定常数,R_i>0(i∈S)为给定矩阵。

注 2  从定义2可以看出,如果d=0,FTB即FTS。因此,FTB可以保证FTS,但反之不成立。

对于系统(9),寻找一个状态反馈u(t)=$\sum\limits_{j=1}^{l}{{}}$K_ix(t)I_｛rt=i｝,使得闭环系统有限时间有界,称为一个FTB问题。

下面的定理给出了系统(8)FTB的一个充分条件。

定理 3  如果对于某个α≥0,存在矩阵Q_i>0,P_i>0,$\forall $i∈S,使得

$\left[ \begin{array}{*{35}{l}} {{Q}_{i}}{{A}_{i}}+A_{i}^{T}{{Q}_{i}}+\sum\limits_{j=1}^{l}{{{q}_{ji}}{{Q}_{j}}}-\alpha {{Q}_{i}}_{i} & {{Q}_{i}}{{G}_{i}} & C_{i}^{T}{{Q}_{i}} \\ * & -\alpha {{P}_{i}} & H_{i}^{T}{{Q}_{i}} \\ * & * & -{{Q}_{i}} \\ \end{array} \right]<0,$

(10)

$\frac{{{c}_{1}}{{\lambda }_{\max }}\left( {{{\bar{Q}}}_{i}} \right)+d\alpha {{\lambda }_{\max }}\left( {{P}_{i}} \right)}{{{\lambda }_{\min }}\left( {{{\bar{Q}}}_{i}} \right)}<\frac{{{c}_{2}}}{{{e}^{\alpha T}}}$

(11)

成立,则系统(8)关于(c₁,c₂,T,R_i,d)有限时间有界。这里${{{\bar{Q}}}_{i}}$=$R_{i}^{-\frac{1}{2}}{{{\bar{Q}}}_{i}}R_{i}^{-\frac{1}{2}}$。

证明  取随机Lyapunov算子V(x,i)=x^TQ_ix(i∈S),式(8)的无穷小生成元

LV(x,i)=2xTQi(Aix+Giv)+(Cix+Hiv)TQi(Cix+Hiv)+$\sum\limits_{j=1}^{l}{{{q}_{ji}}{{x}^{T}}{{Q}_{j}}}$Qjx=[xT,vT]$\left[ \begin{matrix} {{Q}_{i}}{{A}_{i}}+A_{i}^{T}{{Q}_{i}}+C_{i}^{T}{{Q}_{i}}{{C}_{i}}+\sum\limits_{j=1}^{l}{{{q}_{ji}}{{Q}_{j}}} & {{Q}_{i}}{{G}_{i}}+C_{i}^{T}{{Q}_{i}}{{H}_{i}} \\ G_{i}^{T}{{Q}_{i}}+H_{i}^{T}{{Q}_{i}}{{C}_{i}} & H_{i}^{T}{{Q}_{i}}{{H}_{i}} \\ \end{matrix} \right]\left[ \begin{matrix} x \\ v \\ \end{matrix} \right],$

由Schur补,式(10)等价于LV(x,i)<αV(x,i)+αv^TP_iv,由It${\hat{o}}$公式

dV(x,i)=LV(x,i)dt+2xTQi(Cix+Hiv)dw(t),

所以

d[e-αtV(x,i)]=-αe-αtV(x,i)dt+e-αtdV(x,i)= e-αt[ LV(x,i)-αV(x,i)]dt+2e-αtxTQi(Cix+Hiv)dw(t)< αe-αtvTPivdt+2e-αtxTQi(Cix+Hiv)dw(t),

两端从0到t(t∈[0,T])积分,并取期望,得

E[e-αtV(x,i)]-EV(x0,i)<E$\int{_{0}^{t}}$αe-αsvT(s)Piv(s)ds,

两端乘以e^αt,得

EV(x,i)<eαtEV(x0,i)+eαtE$\int{_{0}^{t}}$αe-αsvT(s)Piv(s)ds<eαT[λmax(${{{\bar{Q}}}_{i}}$)E(x0TRx0i)+dαλmax(Pi)]≤ eαT[c1λmax(${{{\bar{Q}}}_{i}}$)+αdλmax(Pi)],

而EV(x,i)=E(x^TQ_ix)≥λ_min(${{{\bar{Q}}}_{i}}$)E(x^TR_ix),因此

E(xTRix)<$\frac{{{e}^{\alpha T}}\left[ {{c}_{1}}{{\lambda }_{\max }}\left( {{{\bar{Q}}}_{i}} \right)+\alpha d{{\lambda }_{\max }}\left( {{P}_{i}} \right) \right]}{{{\lambda }_{\min }}\left( {{{\bar{Q}}}_{i}} \right)},$

显然式(11)成立时,有E(x^TR_ix)<c₂。证毕。

注 3  式(11)可由下列LMI条件来保证:存在正数λ₁,λ₂,使得

I<${{{\bar{Q}}}_{i}}$<λ1I,Pi<λ2I,c1λ1+αdλ2-c2e-αT<0,

成立。

仿照定理2(ⅱ),可以求解系统(9)的FTB问题。

定理 4  如果对于某个α≥0,存在矩阵${{{\bar{Q}}}_{i}}$>0,P_i>0,Y_i,$\forall $i∈S以及正数λ₁,λ₂,使得

$\left[ \begin{matrix} {{\Phi }_{i}}+{{q}_{ii}}{{{\tilde{Q}}}_{i}}-\alpha {{{\tilde{Q}}}_{i}} & {{G}_{i}} & {{{\tilde{Q}}}_{i}}C_{i}^{T}+Y_{i}^{T}D_{i}^{T} & {{\Psi }_{i}} \\ * & -\alpha {{P}_{i}} & H_{i}^{T} & 0 \\ * & * & -{{{\tilde{Q}}}_{i}} & 0 \\ * & * & * & -{{\Theta }_{i}} \\ \end{matrix} \right]<0,$

(12)

λ1I<Qi<I

(13)

Pi<λ2I,

(14)

$\left[ \begin{matrix} \alpha {{\lambda }_{2}}d-{{c}_{2}}{{e}^{-\alpha T}} & 1 \\ 1 & -\frac{{{\lambda }_{1}}}{{{c}_{1}}} \\ \end{matrix} \right]<0,$

(15)

成立,则系统(9)的FTB问题可解,反馈控制器为K_i=Y_i${{{\tilde{Q}}}_{i}}$^-1。式中:Φ_i=A_i${{{\tilde{Q}}}_{i}}$+B_iY_i+${{{\tilde{Q}}}_{i}}$A_i^T+Y_i^TB^T_i; ψ_i=($\sqrt{{{q}_{i1}}}{{{\tilde{Q}}}_{1}}$,…,$\sqrt{{{q}_{ii-1}}}{{{\tilde{Q}}}_{i-1}}$,$\sqrt{{{q}_{ii+1}}}{{{\tilde{Q}}}_{i+1}}$,…,$\sqrt{{{q}_{i1}}}{{{\tilde{Q}}}_{1}}$); Θ_i=diag(${\tilde{Q}}$₁,…,${\tilde{Q}}$_i-1,${\tilde{Q}}$_i+1,…,${\tilde{Q}}$_l),Q_i=$R_{i}^{\frac{1}{2}}{{{\tilde{Q}}}_{i}}R_{i}^{\frac{1}{2}}$。

4 数值例子

例  假设系统(2)含有2个模态,系统矩阵分别为

$\begin{align} & {{A}_{1}}\text{=}\left[ \begin{matrix} 1.23 & 0.78 \\ -3.10 & 0.06 \\ \end{matrix} \right]{{A}_{2}}\text{=}\left[ \begin{matrix} 1.02 & -0.64 \\ 0.73 & 1.46 \\ \end{matrix} \right]{{B}_{1}}\text{=}\left[ \begin{matrix} 2.32 & 2.18 \\ 0.97 & 0.45 \\ \end{matrix} \right]{{B}_{2}}\text{=}\left[ \begin{matrix} 0.42 & -0.11 \\ -0.44 & 1.03 \\ \end{matrix} \right] \\ & {{C}_{1}}\text{=}\left[ \begin{matrix} -1.13 & 0.46 \\ -3.86 & 1.28 \\ \end{matrix} \right]{{C}_{2}}=\left[ \begin{matrix} -1.47 & 0.10 \\ -0.45 & 1.17 \\ \end{matrix} \right],{{D}_{1}}=\left[ \begin{matrix} -0.63 & -3.13 \\ -0.87 & -3.37 \\ \end{matrix} \right],{{D}_{2}}=\left[ \begin{matrix} 1.05 & 1.11 \\ -0.55 & 1.41 \\ \end{matrix} \right] \\ \end{align}$,

转移概率矩阵$\Lambda =\left[ \begin{matrix} -0.6 & 0.6 \\ 0.9 & -0.9 \\ \end{matrix} \right],{{x}_{0}}=\left[ \begin{matrix} 0.50 \\ -0.50 \\ \end{matrix} \right]$。对于给定的常数c₁=1,c₂=12,α=1,R_i=I,T=0.1,应用定理2,可得系统(2)关于(1,12,0.1,I)是FTS能稳的,反馈控制器

${{K}_{1}}=\left[ \begin{matrix} -12.4024 & 0.3773 \\ 2.0763 & 0.1779 \\ \end{matrix} \right],{{K}_{2}}=\left[ \begin{matrix} -0.5661 & 0.9975 \\ 1.7481 & -1.0603 \\ \end{matrix} \right]$

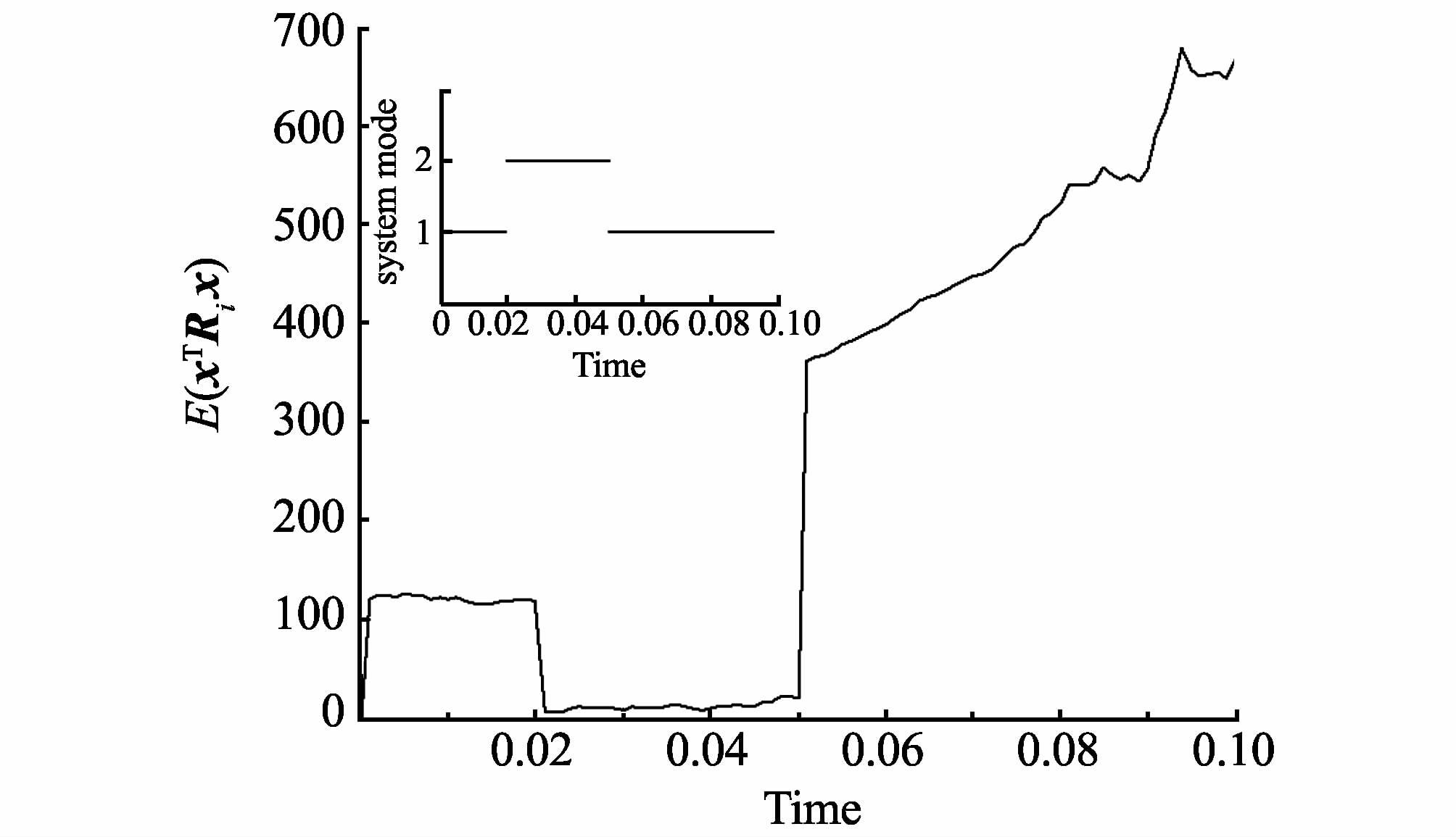
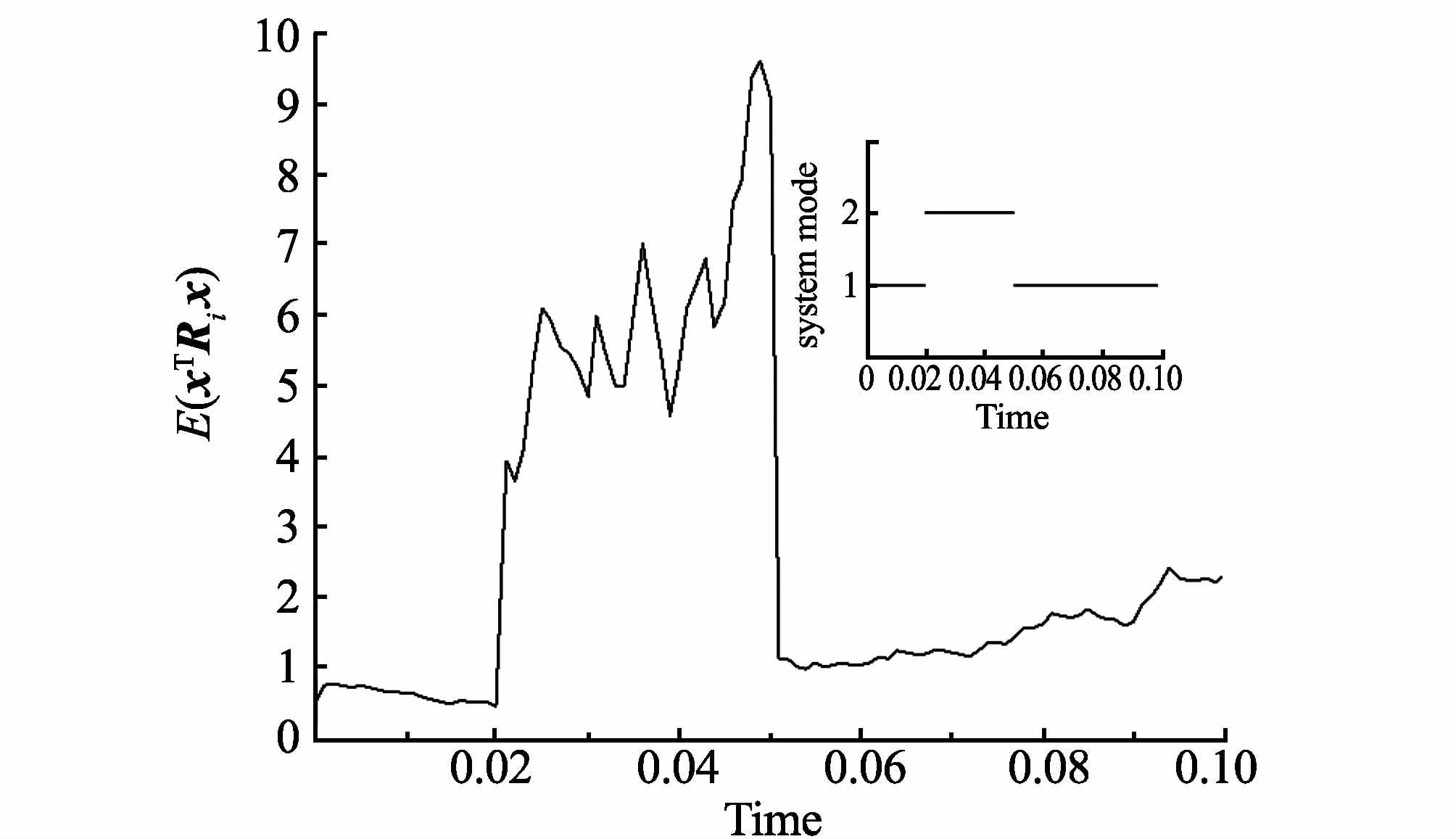
图1、2分别是自治系统和受控系统的仿真图。由图1、2中可以看出系统受控前后有限时间稳定性的情况。

假设系统(9)的转移概率和系统矩阵同上,且

${{G}_{1}}=\left[ \begin{matrix} -0.15 & 2.09 \\ -0.87 & 0.34 \\ \end{matrix} \right],{{G}_{2}}=\left[ \begin{matrix} -1.21 & -0.22 \\ 0.14 & -1.20 \\ \end{matrix} \right],{{H}_{1}}=\left[ \begin{matrix} -0.21 & 0.25 \\ 0.23 & 0.21 \\ \end{matrix} \right],{{H}_{2}}=\left[ \begin{matrix} -3.15 & 0.24 \\ -0.79 & 1.00 \\ \end{matrix} \right]$

对于给定的常数c₁=1,c₂=12,α=1,R_i=I,T=0.1,d=0.01,由定理4,解LMIs(12)～(15),得λ₁=0.119 2,λ₂=235.018 1,因此,系统(9)关于 (1,12,0.1,I,0.01) 的FTB问题可解。反馈控制为

$u\left( t \right)=\left[ \begin{matrix} -105.1915 & -8.3446 \\ 22.912.5 & 2.1445 \\ \end{matrix} \right]x\left( t \right){{I}_{\left\{ {{r}_{t}}=1 \right\}}}+\left[ \begin{matrix} -0.6479 & 1.0056 \\ 1.745.5 & -1.0522 \\ \end{matrix} \right]x\left( t \right){{I}_{\left\{ {{r}_{t}}=2 \right\}}}$

但当c₂=5时,LMIs不可行,但是不能由此判断系统(9)的FTB问题不可解,因为定理4提供的是充分条件,这也是其局限之处。

5 结语

本文将有限时间稳定性的概念推广到应用更为广泛的随机It Markov跳跃系统,给出了系统有限时间随机稳定以及有限时间有界的充分必要条件和充分条件,通过Matlab的LMI求解工具箱可以方便地进行能稳控制器设计。需要指出的是,以上的研究是在转移概率完全已知的前提下进行的。然而,在实际中,要获得精确的状态转移概率是非常困难的。因此,不完全信息下随机Markov 跳跃系统的相关问题将是下一步的研究目标。另外,含乘性噪声的离散随机Markov跳跃系统的情况也有待研究。