2. 山东交通学院信息科学与电气工程学院, 山东 济南 250357
2. School of Information Science and Electrical Engineering, Shandong Jiaotong University, Jinan 250357, Shandong, China
随着电网互联的不断深入,电力系统遭遇各种扰动的可能性增大,稳定性问题逐渐引起研究者的关注[1]。同步发电机励磁控制是改善多机电力系统暂态稳定性的重要手段,在维持机端电压、提髙功率输送极限等方面发挥了关键作用[2],因而,励磁控制策略的研究一直受到电力系统自动控制研究者的广泛关注。
早期的电力系统稳定器(power system stabilizer,PSS) 以及线性最优励磁控制都是基于近似线性化模型,只能在某个平衡点很小的邻域内发挥作用,适用于改善小干扰稳定问题[3, 4, 5, 6]。近年来,反馈线性化[2]、反步法[7]、哈密尔顿系统理论[8]、模糊理论[9]、预测控制[10]等方法应用于多机电力系统励磁控制。例如,文献[2]将机端电压偏差、角速度偏差和有功功率偏差作为状态变量,采用输出反馈方式设计了多机励磁控制器,不需要测量转子角,能较好地抑制扰动并实现机端电压调节;文献[11]基于部分反馈线性化和非线性观测器实现励磁控制,但是没有考虑电力系统模型不确定性;文献[8]建立了广域测量电力系统的非线性时滞广义 Hamilton 模型,设计出广域阻尼控制器,但未能考虑多机系统的广义Hamilton 模型中的耗散项;赵洪山等结合预测控制与模型降阶方法,解决了最优励磁控制和传统PSS无法考虑系统复杂状态和控制输入约束的问题[10];文献[12]提出了基于模糊逼近的间接自适应分散H∞跟踪控制,将建模误差和外部干扰控制在期望指标之内;文献[1]基于改进协同控制方法提高暂态稳定性和调节机端电压,但是也忽略了系统不确定因素。
当多机电力系统励磁控制系统存在参数摄动、测量误差和外部干扰时,改善系统鲁棒性的一种有效方法是滑模控制[13]。文献[14]结合L2增益干扰抑制、自适应逆推法和终端滑模能够快速抑制功率振荡,但是没有考虑快速终端滑模的奇异问题。文献[15]以电机转差率为输出,设计分散式滑模电力系统稳定器,改善系统阻尼特性,然而该控制系统采用线性化模型。文献[16]基于非线性滑模面设计了PSS和自动电压调节器(auto voltage regulator,AVR),能较好调节机端电压,但是,所采用系统模型阶次较高,设计过程复杂,而且没有采取措施削弱励磁电压抖振。文献[17]提出了一种消除趋近过程的模糊滑模励磁方法,然而,其在维持机端压方面表现不好。文献[18]利用模糊逻辑逼近电力系统未知项,用比例积分削弱滑模抖振,设计了一种电力系统稳定器,但并没有说明电磁功率的二阶微分计算方法。
高阶滑模是目前滑模控制理论的研究热点[19, 20, 21],在保留传统滑模优点的同时,消除了相对阶限制、提高滑模精度、削弱控制抖振。近年来,高阶滑模在电力系统已有应用[22, 23, 24, 25, 26, 27],文献[25]基于高阶滑模提高电力系统暂态稳定性,代替传统PSS和AVR作用,在三相短路故障和系统参数变化时,多机系统的功角、转子角速度、端电压都能快速稳定在工作点,但是,该方法不能任意调节收敛时间,并且励磁电压抖振明显。文献[26]针对多机电力系统7阶模型,结合块控制和二阶滑模削弱了控制抖振、实现转子速度稳定和端电压调节,但是其没有规范证明整个闭环系统稳定性。文献[27]设计了高阶滑模励磁控制器,但在多机系统模型应用微分几何时出现了错误,并且励磁电压抖振现象明显。
本研究针对多机电力系统励磁控制模型,考虑系统不确定性以及现有高阶滑模励磁控制抖振严重等问题,提出一种连续高阶滑模分散励磁控制方法。在多机系统受到三相短路故障后,为了使各发电机功角、转子角速度、机端电压能够在排除故障后快速维持在初始工作点,首先把多机电力系统高阶滑模励磁控制问题转换为不确定多机系统有限时间稳定问题,其次,结合几何齐次理论和二阶滑模,利用齐次连续控制律实现功角、转子角速度、端电压有限时间收敛,用超螺旋二阶滑模算法抑制不确定性,既保证整个励磁电压的连续性、削弱了控制抖振,又实现了系统鲁棒性。再次,分析证明了闭环系统的有限时间稳定性。然后,采用精确鲁棒微分器在线计算同步发电机功角的一阶、二阶微分。最后,对本研究所提控制方法和文献[25]算法在三相短路故障下仿真试验,验证算法的适用性、有效性。
1 多机电力系统模型描述
假设各发电机机械功率保持不变,采用快速励磁,在同步坐标系下,n机电力系统第i台发电机的数学模型为[14, 25]
$\left\{ \begin{align}
& {{{\dot{\delta }}}_{i}}={{\omega }_{i}}-{{\omega }_{s}}; \\
& {{{\dot{\omega }}}_{i}}=-\frac{{{D}_{i}}}{2{{H}_{i}}}\left( {{\omega }_{i}}-{{\omega }_{s}} \right)+\frac{{{\omega }_{s}}}{2{{H}_{i}}}\left( {{P}_{mi}}-{{P}_{ei}} \right)+{{d}_{i1}}+\left( t \right); \\
& \dot{E}_{qi}^{'}=\frac{1}{T_{di}^{'}}({{E}_{fi}}-{{E}_{qi}}+({{X}_{di}}-X_{di}^{'}){{I}_{di}})+{{d}_{i2}}. \\
\end{align} \right.$
(1)
系统相关电气量为:
Iqi=GiiE′qi+$\sum\limits_{j = 1,j \ne i}^n {} $E′qj {Gijcos(δj-δi)-
Bijsin(δj-δi)}
(2)
Idi=-BiiE′qi-$\sum\limits_{j = 1,j \ne i}^n {} $E′qj {Gijsin(δj-δi)+Bijcos(δj-δi)},
(3)
Pei=E′qi Iqi,
(4)
Vdi=XqiIqi,
(5)
Vqi=E′qi-X′di Idi,
(6)
Vti=$\sqrt {\left( {V_{di}^2 + V_{qi}^2} \right)} ,$
(7)
$\left\{ {\begin{array}{*{20}{c}}
{\left| {{d_{i1}}\left( t \right)} \right| \leqslant {d_{i1M}},\left| {{d_{i2}}\left( t \right)} \right| \leqslant {d_{i2M}};} \\
{\left| {{{\ddot d}_{i1}}\left( t \right)} \right| \leqslant {d_{i1s}},\left| {{{\dot d}_{i2}}\left( t \right)} \right| \leqslant {d_{i2f}}.}
\end{array}} \right.$
(8)
选取多机电力系统中第i子系统的状态向量xi=[xi,1 xi,2 xi,3]T=[δi ωi-ωs E′qi]T
,控制输入ui=Efi
,则:
$\left\{ \begin{align}
& {{{\dot{x}}}_{i,1}}={{x}_{i,2}}; \\
& {{{\dot{x}}}_{i,2}}=-\frac{{{D}_{i}}}{2{{H}_{i}}}{{x}_{i,2}}+\frac{{{\omega }_{s}}}{2{{H}_{i}}}\left( {{P}_{mi}}-{{x}_{i,3}}{{I}_{qi}} \right)+{{d}_{il}}\left( t \right); \\
& {{{\dot{x}}}_{i,3}}=\frac{1}{T_{di}^{'}}(-{{x}_{i.3}}+({{X}_{di}}-X_{di}^{'}){{I}_{di}})+\frac{1}{T_{di}^{'}}{{u}_{i}}+{{d}_{i2}}\left( t \right). \\
\end{align} \right.$
(9)
选取滑模变量σi=δi-δi*=xi,1-δi*,δi*是发电机功角设定值,计算可得式(9)关于滑模变量σi的相对阶为3,即:
σi(3)=f(xi,t)+g(xi,t)ui+di=$\begin{align}
& \underbrace{\frac{{{\omega }_{s}}}{2{{H}_{i}}T_{di}^{'}}\left( {{I}_{qi}}{{x}_{i,3}} \right.-\left( {{X}_{di}}-X_{di}^{'} \right)\left. {{I}_{di}}{{I}_{qi}} \right)}_{{{f}_{1}}}+\underbrace{\frac{{{D}_{i}}{{\omega }_{s}}}{4H_{i}^{2}}\left( {{P}_{mi}}-{{x}_{i,3}}{{I}_{qi}} \right)-\frac{{{\omega }_{s}}}{2{{H}_{i}}}{{x}_{i,3}}{{{\dot{I}}}_{qi}}}_{{{f}_{2}}}+ \\
& \underbrace{\frac{D_{i}^{2}}{4H_{i}^{2}}{{x}_{i,2}}}_{{{f}_{3}}}-\underbrace{\frac{{{\omega }_{s}}{{I}_{qi}}}{2{{H}_{i}}T_{di}^{'}}}_{g\left( {{x}_{i}},t \right)}{{u}_{i}}-\underbrace{\frac{{{D}_{i}}}{2{{H}_{i}}}{{d}_{i1}}\left( t \right)}_{{{d}_{ia}}}+\underbrace{{{{\dot{d}}}_{i1}}\left( t \right)-\frac{{{\omega }_{s}}{{I}_{qi}}}{2{{H}_{i}}}{{d}_{i2}}\left( t \right)}_{{{d}_{ib}}}, \\
\end{align} $
(10)
对式(10)施加反馈控制:
ui=g(xi,t)-1(-f(xi,t)+νi),
(11)
σi(3)=νi+di,
(12)
$\left\{ {\begin{array}{*{20}{c}}
{{{\dot z}_{i,1}} = {z_{i,2}};} \\
{{{\dot z}_{i,2}} = {z_{i,3}};} \\
{{{\dot z}_{i,3}} = {v_i} + {d_i}.}
\end{array}} \right.$
(13)
实现具有不确定性积分链系统的有限时间稳定是一个复杂的任务[28]。为了完成控制目标、保证系统鲁棒性、实现励磁电压控制连续和抖振削弱,本研究中辅助控制律νi由齐次控制律νnomi和二阶滑模控制项两部分组成,首先引入文献[29]可构造的齐次连续控制算法νnomi 。
2.1 齐次连续控制律
当不考虑多机系统发电机参数不确定性、测量误差、外部干扰等因素,即di=0,则式(13)转变为标称3重积分链:
$\left\{ {\begin{array}{*{20}{c}}
{{{\dot z}_{i,1}} = {z_{i,2}};} \\
{{{\dot z}_{i,2}} = {z_{i,3}};} \\
{{{\dot z}_{i,3}} = {v_i}.}
\end{array}} \right.$
(14)
针对此类标称积分链,文献[29]提出了一种有限时间收敛算法。
引理 1[29] 选择正常数αi,1
、αi,2
、αi,3
,使得p3+αi,3p2+αi,2p+αi,1
是霍尔维茨多项式,则存在qi∈(0,1),使得对任意li∈(1-qi,1)
,在反馈控制式(15)作用下式(14)于有限时间稳定在原点。
νnomi=-αi,1sign(zi,1)zi,1li,1-αi,2sign(zi,2)zi,2li,2-αi,3sign(zi,3)zi,3li,3,
(15)
控制律式(15)是连续的,能够保证标称系统式(14)有限时间稳定,继而实现了对式(1)不包含不确定项的有限时间控制,但是,实际的多机电力系统不但各机参数会随时间变化,各子系统之间也会相互作用,对于各子系统,可以把这些不确定性看作干扰项,下面采用二阶滑模实现系统的鲁棒性。
2.2 鲁棒性实现本研究所提出的高阶滑模控制算法分为两步,即控制律νnomi保证标称系统式(14)有限时间稳定,二阶滑模控制律νsi(zi,zauxi)确保式(13)的鲁棒性。
为了实现不确定积分链式(13)的有限时间稳定,设计如下控制律:
| $\left\{ {\begin{array}{*{20}{c}} {{v_i} = {v_{nomi}} + {v_{si}}\left( {{z_i},{z_{auxi}}} \right);} \\ {{{\dot z}_{auxi}} = { - _{nomi}}.} \end{array}} \right.$ | (16) |
定义新的滑模变量si为
| si=zi,3+zauxi。 | (17) |
对si
求导数,得
${{\dot s}_i} = {{\dot z}_{i,3}}{{\dot z}_{auxi}}$=νi+di-νnomi=di+νsi。
(18)
针对式(18)系统,采用一阶滑模控制律νsi=Ksign(si) 可实现有限时间内si→0,但是这样会使控制量存在严重抖振,阻碍实际应用。超螺旋二阶滑模把不连续切换控制包含在积分项,使得控制量是连续的,大大削弱控制抖振。
二阶滑模超螺旋算法[30]
$\left\{ {\begin{array}{*{20}{c}}
{{v_{si}} = - {\lambda _i}{{\left| {{s_i}} \right|}^{1/2}}sign\left( {{s_i}} \right) + {v_{1si}};} \\
{{{\dot v}_{1si}} = \left\{ { - {v_{si}},\left| {{v_{si}}} \right| > {U_{Mi}};} \right.} \\
{ - {\gamma _i}sign\left( {{s_i}} \right),\left| {{v_{si}}} \right| \leqslant {U_{Mi}}.}
\end{array}} \right.$
(19)
下面给出本研究中重要结论。
定理 1 针对多机电力系统式(1),假设系统不确定性满足式(8),若控制律设计为
ui=g-1(xi,t)[-f(xi,t)+νnomi+νsi],
(20)
证明 依据超螺旋二阶滑模有限时间稳定条件[30],针对式(18) 系统,考虑式(8),因为存在一些正常数Ci,KMi,Kmi,UMi和ρi
使得式(21)成立,
$\left\{ {\begin{array}{*{20}{c}}
{\left| {{{\dot d}_i}} \right| \leqslant \left| {{{\dot d}_{ia}}} \right| + \left| {{{\dot d}_{ib}}} \right| \leqslant {C_i};} \\
{0 \leqslant {K_{mi}} \leqslant \varphi \leqslant {K_{Mi}};} \\
{\left| {{d_i}} \right| \leqslant {\rho _i}{U_{Mi}},0 < {\rho _i} < 1.}
\end{array}} \right.$
(21)
那么,超螺旋算法控制参数的选取如果满足:
$\left\{ {\begin{array}{*{20}{c}}
{{\gamma _i} > \frac{{{C_i}}}{{{K_{mi}}}},} \\
{{\lambda _i} > \sqrt {\frac{2}{{{K_{mi}}{\gamma _i} - {C_i}}}} \frac{{\left( {{K_{mi}}{\gamma _i} + {C_i}} \right){K_{Mi}}\left( {1 + {\rho _i}} \right)}}{{K_{mi}^2}},}
\end{array}} \right.$
(22)
尽管存在不确定项di
,式(19)控制律保证了系统轨迹有限时间到达并保持在二阶滑模s=${\dot s}$=0上,则依据${\dot s}$=0得出等效控制
νsieq=-di。
(23)
把νi=νnomi+νsieq代入式(13),可以得到类似于式(14)的等效闭环动态,因为控制律νnomi是利用引理1设计,系统轨迹有限时间收敛到零,因此,在有限时间建立了σ的3阶滑动模态,多机电力系统各状态也实现了有限时间稳定。
注: 从观测器的角度理解,二阶滑模超螺旋控制律νsi也可以看作不确定项di的观测器。
为了执行式(20)控制律,要实时精确计算或测量σi、${\dot \sigma }$i、${\ddot \sigma }$i,本研究采用文献[30]的精确鲁棒微分器对它们在线计算:
$\left\{ {\begin{array}{*{20}{l}}
{{{\dot \mu }_{i,0}} = {v_{i,0}};} \\
{{v_{i,0}} = - {\rho _{i,3}}L_i^{1/3}{{\left| {{\mu _{i,0}} - {\sigma _i}} \right|}^{2/3}}sign\left( {{\mu _{i,0}} - {\sigma _i}} \right) + {\mu _{i,1}};} \\
{{{\dot \mu }_{i,1}} = {v_{i,1}};} \\
{{v_{i,1}} = - {\rho _{i,2}}L_i^{1/2}{{\left| {{\mu _{i,1}} - {v_{i,0}}} \right|}^{1/2}}sign\left( {{\mu _{i,1}} - {v_{i,0}}} \right) + {\mu _{i,2}};} \\
{{{\dot \mu }_{i,2}} = - {\rho _{i,1}}{L_i}sign\left( {{\mu _{i,2}} - {v_{i,1}}} \right).}
\end{array}} \right.$
(24)
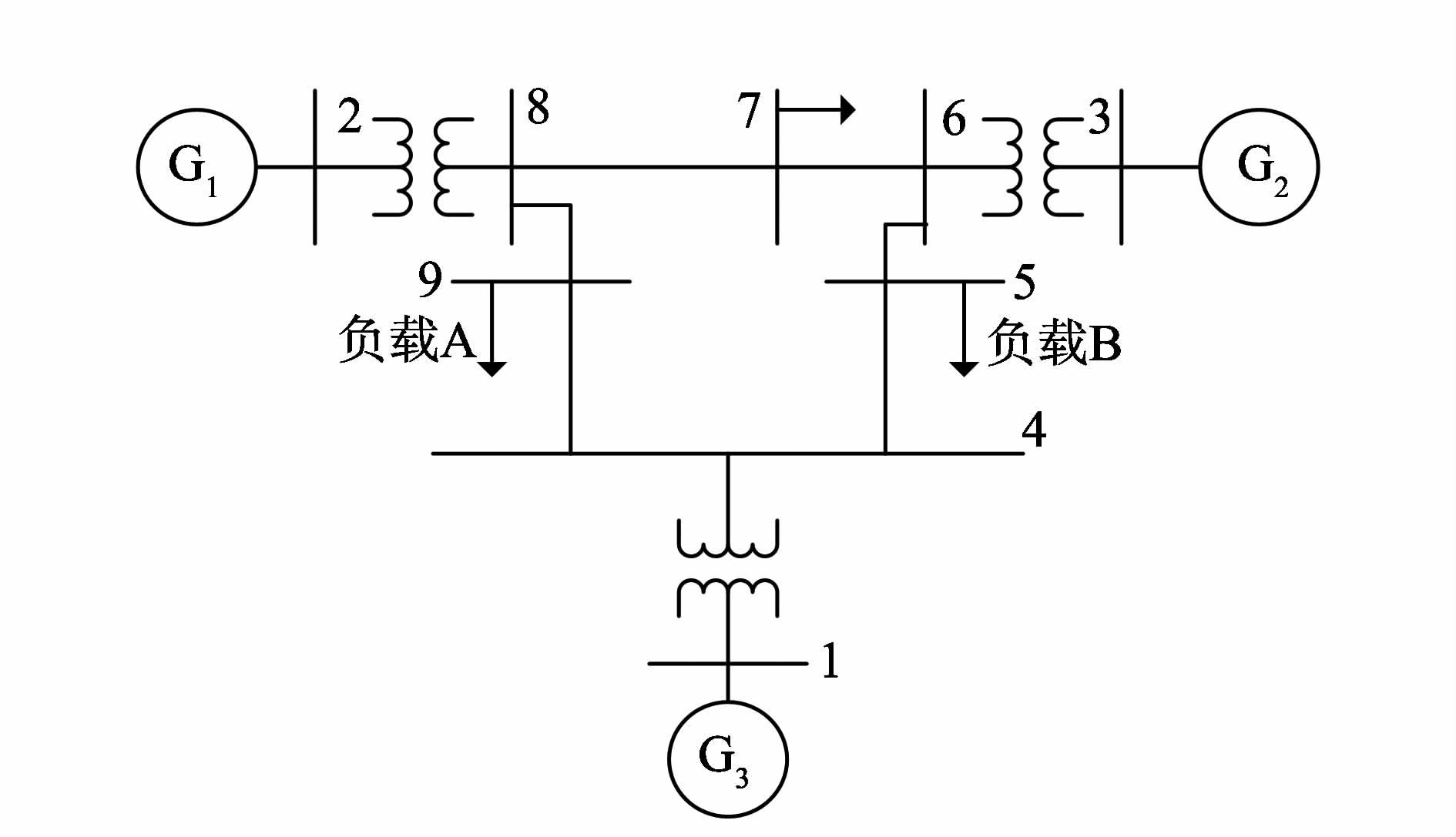
考虑如图1所示3 机 9 节点电力系统,各发电机参数标称值如表1,节点导纳矩阵为
${G_{ij}} = \left[ {\begin{array}{*{20}{c}}
{0.8453}&{0.2870}&{0.2095} \\
{0.2870}&{0.4199}&{0.2132} \\
{0.2095}&{0.2132}&{0.2770}
\end{array}} \right],{B_{ij}} = \left[ {\begin{array}{*{20}{c}}
{ - 2.9882}&{1.5130}&{1.2256} \\
{1.5130}&{ - 2.7238}&{1.0879} \\
{1.2256}&{1.0879}&{ - 2.3681}
\end{array}} \right],$
|
图1 三机电力系统 Fig.1 Three-machine power system |
| 表1 发电机标称参数 Table 1 Nominal parameters of generators |
励磁电压限幅为|Efi|≤4pu,系统运行点为
$\left\{ {\begin{array}{*{20}{c}}
{x_{1,1}^* = 0.0396}&{x_{1,2}^* = 0}&{x_{1,3}^* = 1.06;} \\
{x_{2,1}^* = 0.3444}&{x_{2,2}^* = 0}&{x_{2,3}^* = 0.95;} \\
{x_{3,1}^* = 0.2300}&{x_{3,2}^* = 0}&{x_{3,3}^* = 1.58.}
\end{array}} \right.$
假设系统不确定性为di1(t)=0.01sin8t+0.006cos10t ,di2(t)=0.01sin10t,分析系统参数,结合式(8)、式(21)和式(22),控制器参数选择为li,1=0.5 ,li,2=0.6,li,3=0.75,αi,1=1 ,αi,2=1.5,αi,3=1.5,UM=2,λi=3.5 ,γi=1.7 ,鲁棒微分器参数Li=500 。
为了比较控制性能,采用文献[25]算法进行仿真对比,其齐次高阶滑模励磁控制律设计为
${u_i} = - 4\frac{{{z_{i,2}} + 2{{\left( {\left| {{z_{i,1}}} \right| + {{\left| {{z_{i,0}}} \right|}^{2/3}}} \right)}^{ - 1/2}}\left( {{z_{i,1}} + {{\left| {{z_{i,0}}} \right|}^{2/3}}sign\left( {{z_{i,0}}} \right)} \right)}}{{\left| {{z_{i,2}}} \right| + 2{{\left( {\left| {{z_{i,1}}} \right| + {{\left| {{z_{i,0}}} \right|}^{2/3}}} \right)}^{1/2}}}}.$
(25)
系统从平衡工作点开始运行,仿真步长设置为0.001 s,在t=0.8 s时,1号发电机和3号发电机联络线靠近1号发电机的输电线路发生瞬时三相对地短路故障,在t=0.883 s时故障消失。
三相短路故障发生在同步电机机端时,故障期间该发电机不提供任何功率,而且,由于欠阻尼作用,电力系统在故障排除后有可能变得不稳定。图2~7为两种励磁控制器情况下仿真结果。分析可知,两种控制算法都能克服系统有界不确定项di1,di2的影响,使得系统各发电机功角、发电机转子相对角速度、端电压稳定在故障前的设定值。
|
图2 发电机功角 Fig.2 Power angle |

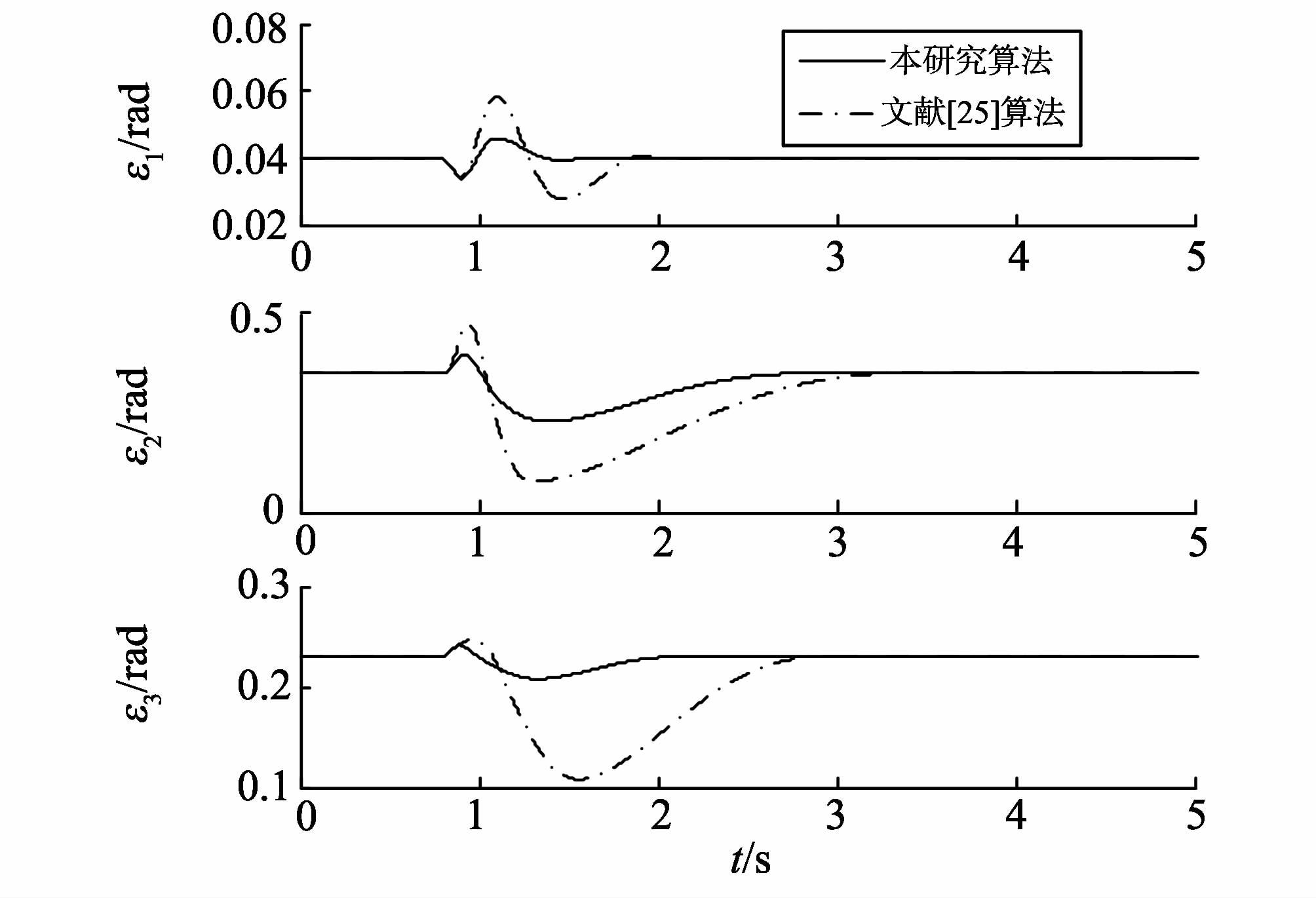
|
图3 发电机转子相对角速度 Fig.3 Relative angular velocity |
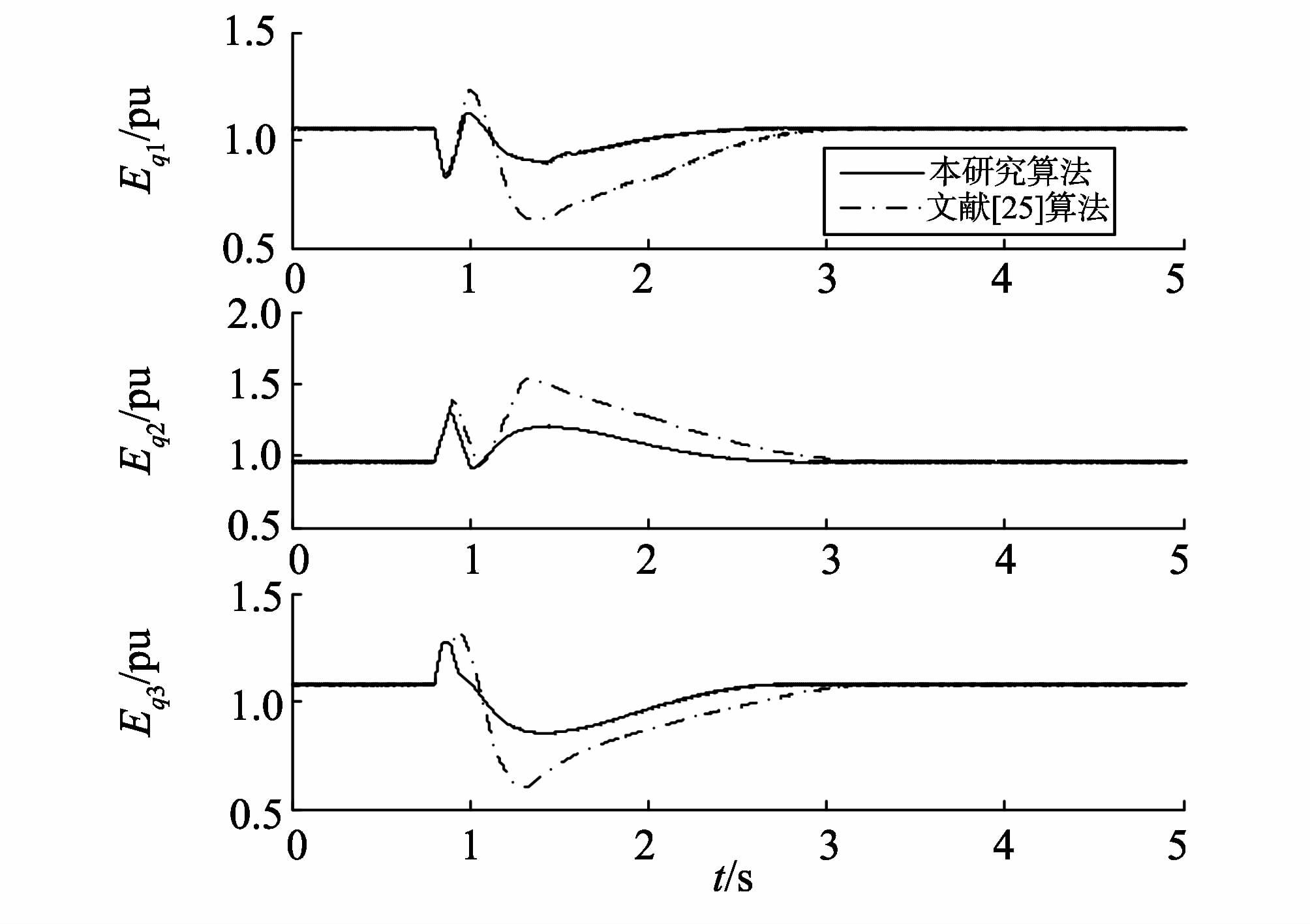
|
图4 发电机q轴暂态电动势 Fig.4 Quadrature-axis transient electromotive force |
|
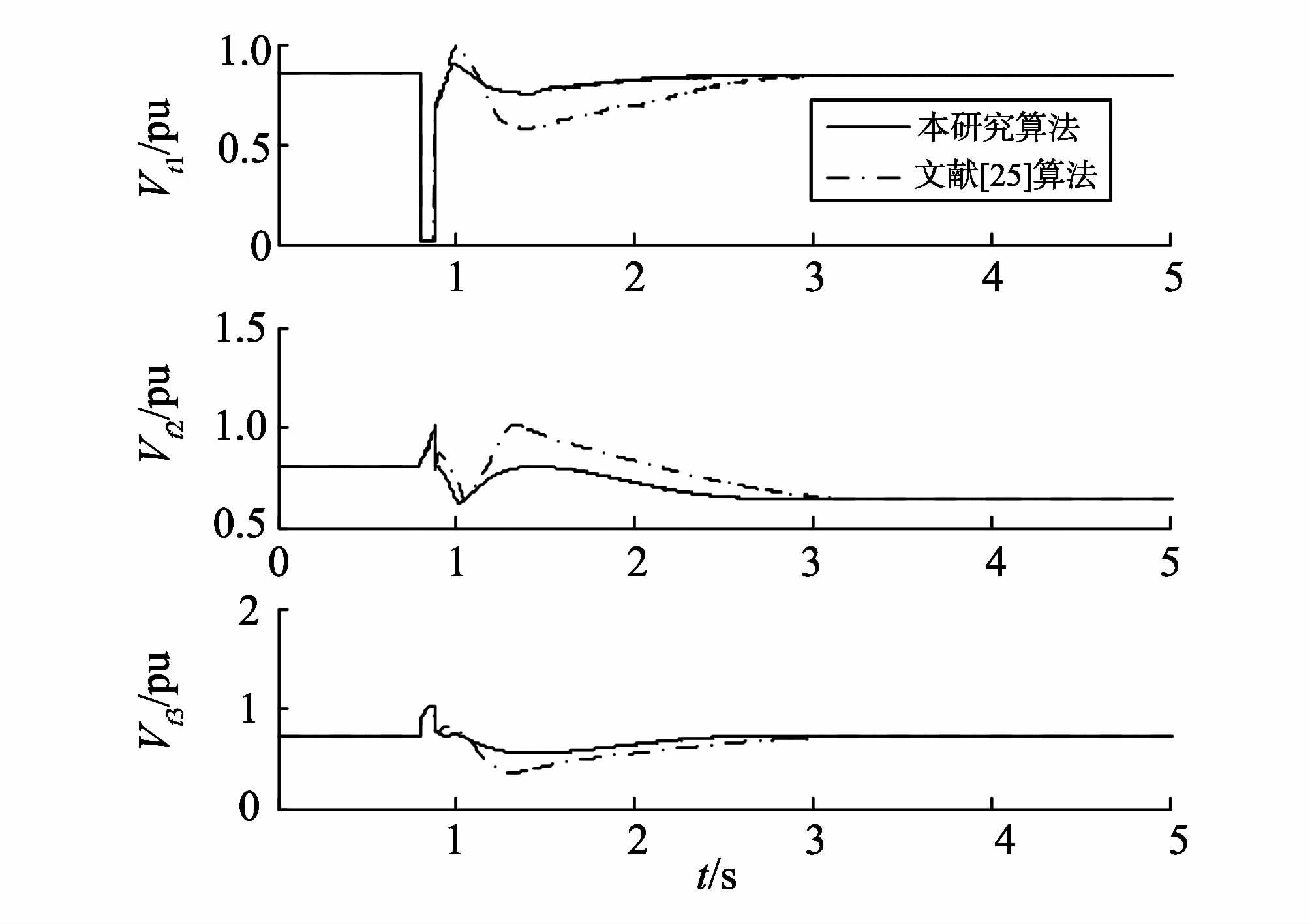
图5 发电机端电压 Fig.5 Terminal voltage |
|
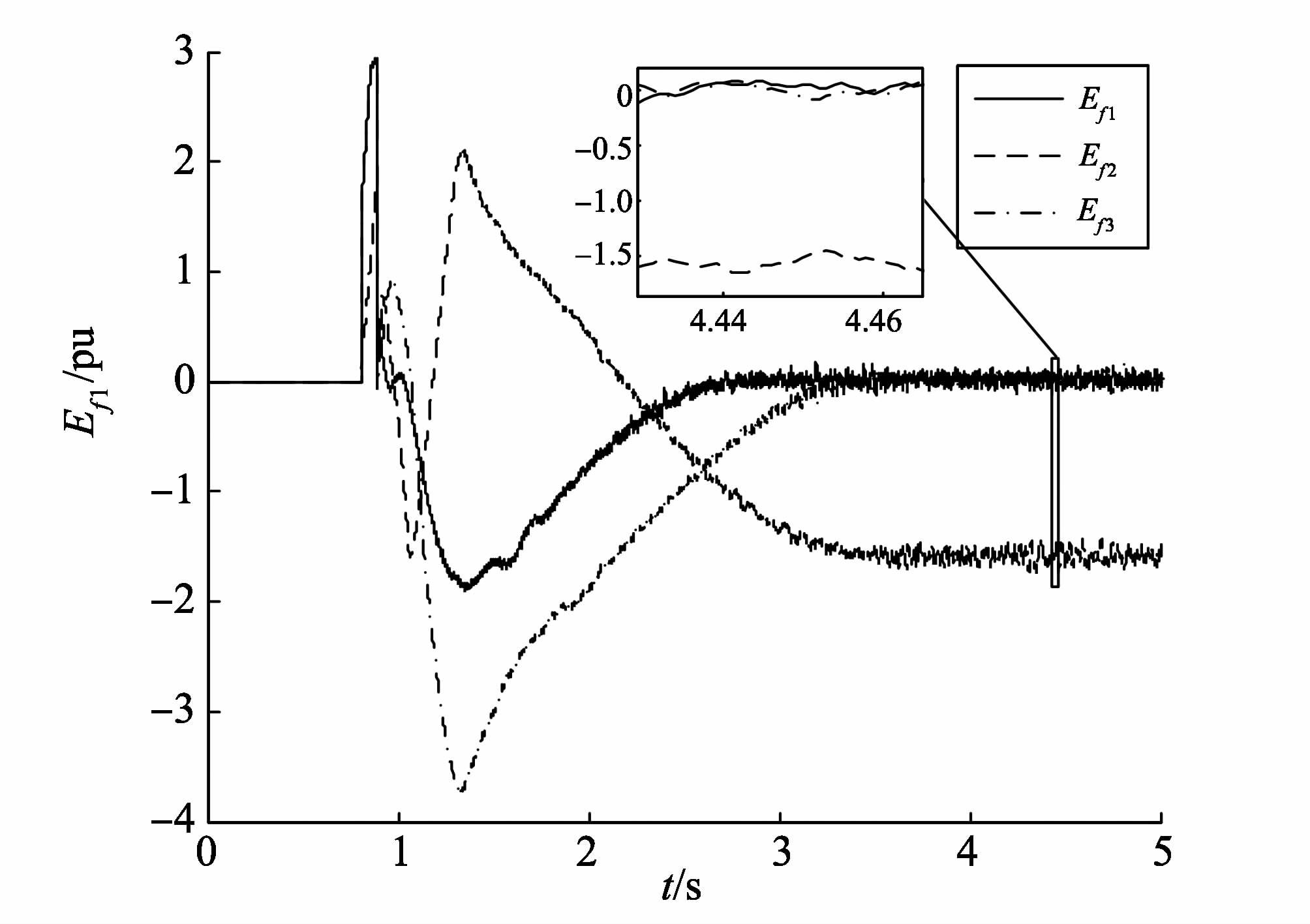
图7 本研究算法下的励磁电压 Fig.7 Exciting voltage under the proposed algorithm |
图2所示为发电机功角响应,两种控制方法都能使其稳定在故障前平衡工作点,但是,在本研究所提出的连续高阶滑模励磁控制器下,3台发电机分别在1.8、2.6、2 s时刻就恢复到故障前的值,功角响应更快,在本研究所提出的算法下,超调值也更小,如1号发电机,在文献[25]齐次高阶滑模算法下,最大超调量为0.020,而在本研究连续高阶滑模励磁算法下量,最大超调量为0.007。
因为同步发电机工作在同步转速,在正常工作条件下速度偏移为0,但是当故障发生时,电机转速也会受到扰动。图3为发电机转子相对角速度响应曲线,分析图3可知,两种控制算法下,故障恢复后,电机转速偏移都为0,但是,在本研究所提出的算法下,发电机转子趋于稳定的速度更快,波动更小。
发电机q轴暂态电动势响应曲线如图4所示,两种控制算法下都能使得发电机q轴暂态电动势稳定到故障前的值:1.06、0.95和1.58 pu,但是,在本研究提出的控制算法下,其波动幅值小、恢复到故障前稳态的时间短。
图5给出了发电机端电压响应曲线,分析图5可知,在三相短路故障恢复后,基于本研究所提出的励磁方法下,1号发电机端电压在1.25 s时刻,2号发电机在1.48 s时刻,3在发电机在1.21 s时刻即恢复至故障前稳态值0.72、0.65和0.82 pu,而在文献[25]齐次高阶滑模励磁控制下,各端电压暂态过程更长,超调值更大。
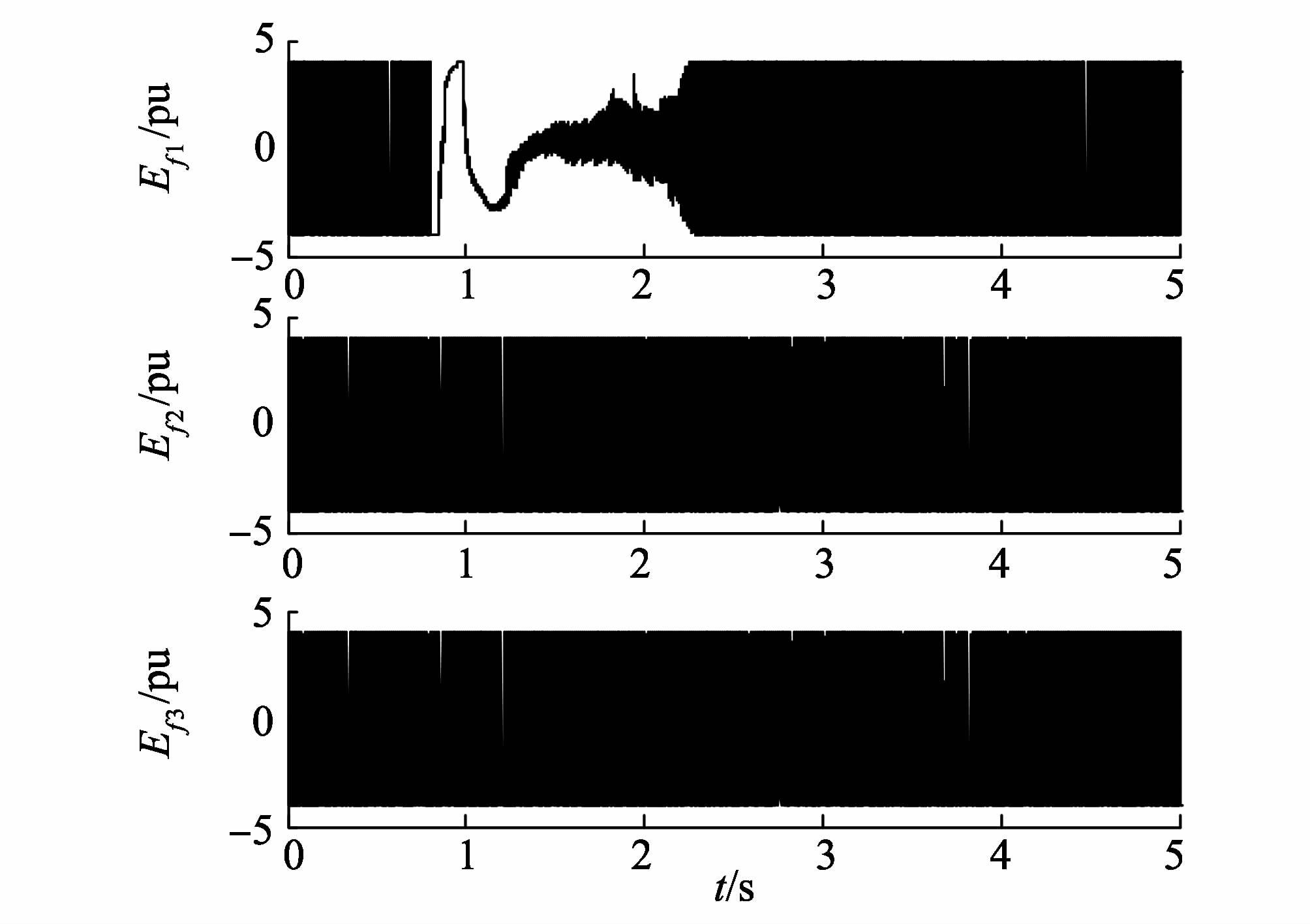
在文献[25]齐次高阶滑模算法下的控制输入,即发电机励磁电压的响应曲线如图6所示,控制量在上下幅值±4 pu高频切换,这也是该算法的最大缺点,因为目前电力电子器件切换频率达不到这么高,这会影响控制效果,再者,如此高频的切换速度会严重缩短励磁器的使用寿命。
图7是本研究所提方案的励磁电压,事实上,正如前文所分析的,辅助控制νi中的齐次控制项和二阶滑模超螺旋控制律两部分都是连续的,因此,如图7所示,励磁控制电压是连续的,当发生短路故障时,励磁电压接近幅值±4 pu,但是,当各发电转子速度、功角、端电压趋于稳定时,励磁电压幅值基本保持在±1 pu范围内,虽然由于不确定因素的存在、各发电机互联影响,励磁电压会有小幅波动,但是,因为整个励磁控制电压是连续的,而且,系统鲁棒控制项,即二阶滑模部分抖振得以抑制,因此,励磁电压颤动频率和幅值都明显削弱,此外,由图7的局部放大图也可以看出,励磁控制电压变化连续、平滑,高频抖振现象几乎消除。
4 结论针对具有不确定性的多机电力系统励磁控制问题,提出一种连续高阶滑模控制方法。高阶滑模控制问题等效转化为有限时间稳定问题,反馈控制中辅助控制项由齐次连续控制律和超螺旋二阶滑模控制两部分实现。在三相短路故障下进行了仿真试验,结果表明本研究提出的控制方法能提高多机系统暂态稳定性,励磁控制电压作用连续、抖振小,而且,对多机电力系统参数摄动、测量误差、外部干扰等不确定性具有鲁棒性。
| [1] | ZHAO P, YAO W, WEN J, et al.Improved synergetic excitation control for transient stability enhancement and voltage regulation of power systems[J].International Journal of Electrical Power & Energy Systems, 2015, 68:44-51.( 2) 2) |
| [2] | 阮阳, 袁荣湘.采用输出反馈方式的电力系统非线性励磁控制[J]. 中国电机工程学报, 2011, 31(34):68-76. RUAN Yang, YUAN Rongxiang. Output feedback based nonlinear excitation control for power systems[J]. Proceedings of the CSEE, 2011, 31(34):68-76.(  3) 3) |
| [3] | KUNDUR P. Power system stability and control[M].NewYork: McGraw-Hill, 1994:813-814.( 1) 1) |
| [4] | GURRALA G, SEN I.Power system stabilizers design for interconnected power systems[J].IEEE Transactions on Power Systems, 2010, 25(2):1042-1051.( 1) 1) |
| [5] | HOSSAIN M J, POTA H R, UGRINOVSKII V A, et al. Voltage mode stabilisation in power systems with dynamic loads[J]. International Journal of Electrical Power & Energy Systems, 2010, 32(9):911-920.( 1) 1) |
| [6] | 阮阳, 袁荣湘, 万黎, 等. 同步发电机的非线性鲁棒电压控制[J]. 电工技术学报, 2012, 27(9):9-16. RUAN Yang, YUAN Rongxiang, WAN Li, et al. Nonlinear robust voltage control for synchronous generators[J]. Transactions of China Electrotechnical Society, 2012, 27(9):9-16.(  1) 1) |
| [7] | 兰洲,甘德强,倪以信,等.电力系统非线性鲁棒自适应分散励磁控制设计[J].中国电机工程学报,2006,31(13):33-39. LAN Zhou, GAN Deqiang, NI Yixin, et al. Decentralized nonlinear robust adaptive excitation control design for power systems[J].Proceedings of the CSEE, 2006, 31(13):33-39.(  1) 1) |
| [8] | 古丽扎提. 海拉提, 王杰. 广义 Hamilton 多机电力系统的广域时滞阻尼控制[J].中国电机工程学报,2014,34(34):6199-6208. GULIZHATI Hailati, WANG Jie. Wide-area time-delay damping control of generalized hamilton multi-machine power system[J]. Proceedings of the CSEE, 2014, 34(34):6199-6208.(  2) 2) |
| [9] | GHASEMI A, SHAYEGHI H, ALKHATIB H. Robust design of multimachine power system stabilizers using fuzzy gravitational search algorithm[J]. International Journal of Electrical Power & Energy Systems, 2013, 51:190-200.( 1) 1) |
| [10] | 赵洪山, 兰晓明, 周雪青. 基于平衡降阶模型的多机系统非线性励磁预测控制[J]. 中国电机工程学报, 2013, 36(22):61-67. ZHAO Hongshan, LAN Xiaoming, ZHOU Xueqing. Nonlinear excitation prediction control of multi-machine power systems based on balanced reduced model[J]. Proceedings of the CSEE, 2013, 36(22):61-67.(  2) 2) |
| [11] | MAHMUD M A, HOSSAIN M J, POTA H R. Transient stability enhancement of multimachine power systems using nonlinear observer-based excitation controller[J]. International Journal of Electrical Power & Energy Systems, 2014, 58:57-63.( 1) 1) |
| [12] | 吴忠强, 宋明厚, 付立元. 多机电力系统间接自适应模糊分散H∞控制研究[J]. 电力自动化设备, 2013, 33(1):23-27. WU Zhongqiang, SONG Minghou, FU Liyuan. Indirect adaptive fuzzy and distributed H∞control for multi-machine power system[J]. Electric Power Automation Equipment, 2013, 33(1):23-27.(  1) 1) |
| [13] | 赵辉, 王亚菲, 王红君, 等. 基于滑模变结构控制的余热发电机机组励磁控制研究[J]. 电力系统保护与控制, 2015, 43(6):8-13. ZHAO Hui, WANG Yafei, WANG Hongjun, et al. Study of waste heat power generation units excitation control based on sliding mode variable structure control[J]. Power System Protection and Control, 2015, 43(6):8-13.(  1) 1) |
| [14] | 邹德虎, 王宝华. 多机电力系统自适应鲁棒 Terminal 滑模励磁控制[J].电力自动化设备, 2011(12):79-82. ZOU Dehu, WANG Baohua. Adaptive and robust excitation control with Terminal sliding mode for multi-machine power system[J]. Electric Power Automation Equipment, 2011(12):79-82.(  2) 2) |
| [15] | BANDAL V, BANDYOPADHYAY B. Robust decentralised output feedback sliding mode control technique-based power system stabiliser (PSS) for multimachine power system[J]. IET Control Theory & Applications, 2007, 1(5):1512-1522.( 1) 1) |
| [16] | HUERTA H, LOUKIANOV A G, CAEDO J M. Decentralized sliding mode block control of multimachine power systems[J]. International Journal of Electrical Power & Energy Systems, 2010, 32(1):1-11.( 1) 1) |
| [17] | NECHADI E, HARMAS M N, HAMZAOUI A, et al. A new robust adaptive fuzzy sliding mode power system stabilizer[J]. International Journal of Electrical Power & Energy Systems, 2012, 42(1):1-7.( 1) 1) |
| [18] | SAOUDI K, HARMAS M N. Enhanced design of an indirect adaptive fuzzy sliding mode power system stabilizer for multi-machine power systems[J]. International Journal of Electrical Power & Energy Systems, 2014, 54:425-431.( 1) 1) |
| [19] | LEVANT A, MICHAEL A. Adjustment of high-order sliding-mode controllers[J]. International Journal of Robust and Nonlinear Control, 2009, 19(15):1657-1672.( 1) 1) |
| [20] | 易伯瑜, 康龙云, 陶思念, 等. 永磁同步电机抗扰高阶滑模观测器设计[J]. 电工技术学报, 2014, 29(5):132-140. YI Boyu, KANG Longyun, TAO Sinian, et al. Design of robust high order sliding mode observer for permanent magnet synchronous motors[J]. Transactions of China Electrotechnical Society, 2014, 29(5):132-140.(  1) 1) |
| [21] | LIU X, HAN Y. Finite time control for MIMO nonlinear system based on higher-order sliding mode[J]. ISA transactions, 2014, 53(6):1838-1846.( 1) 1) |
| [22] | BELTRAN B, EL HACHEMI BENBOUZID M, AHMED-ALI T. Second-order sliding mode control of a doubly fed induction generator driven wind turbine[J]. IEEE Transactions on Energy Conversion, 2012, 27(2):261-269.( 1) 1) |
| [23] | LIU J, LAGHROUCHE S, WACK M. Observer-based higher order sliding mode control of power factor in three-phase AC/DC converter for hybrid electric vehicle applications[J]. International Journal of Control, 2014, 87(6):1117-1130.( 1) 1) |
| [24] | EVANGELISTA C, VALENCIAGA F, PULESTON P. Active and reactive power control for wind turbine based on a MIMO 2-sliding mode algorithm with variable gains[J]. IEEE Transactions on Energy Conversion, 2013, 28(3):682-689.( 1) 1) |
| [25] | COLBIA-VEGA A, DE LEON-MORALES J, FRIDMAN L, et al. Robust excitation control design using sliding-mode technique for multimachine power systems[J]. Electric Power Systems Research, 2008, 78(9):1627-1634.( 7) 7) |
| [26] | HUERTA H, LOUKIANOV A G, CANEDO J M. Robust multimachine power systems control via high order sliding modes[J]. Electric Power Systems Research, 2011, 81(7):1602-1609.( 2) 2) |
| [27] | BENAHDOUGA S, BOUKHETALA D, BOUDJEMA F. Decentralized high order sliding mode control of multimachine power systems[J]. International Journal of Electrical Power & Energy Systems, 2012, 43(1):1081-1086.( 2) 2) |
| [28] | DEFOORT M, FLOQUET T, KOKOSY A, et al. A novel higher order sliding mode control scheme[J]. Systems & Control Letters, 2009, 58(2):102-108.( 1) 1) |
| [29] | BHAT S P, BERNSTEIN D S. Geometric homogeneity with applications to finite-time stability[J].Mathematics of Control, Signals and Systems, 2005, 17(2):101-127.( 2) 2) |
| [30] | 赵占山, 张静, 孙连坤, 等. 有限时间收敛的滑模自适应控制器设计[J]. 山东大学学报(工学版), 2012, 42(4):74-78. ZHAO Zhanshan, ZHANG Jing, SUN Liankun, et al. Design of self-adaptive sliding mode controller with finite time convergence [J]. Journal of Shandong University (Engineering Science), 2012, 42(4):74-78.(  3) 3) |