2. 安徽理工大学经济与管理学院, 安徽 淮南 232001
2. School of Economics and Management, Anhui University of Science and Technology, Huainan 232001, Anhui, China
随着互联网技术和信息技术的迅猛发展,互联网上的信息量急剧上升,用户快速搜到所需要的信息日益困难。推荐系统能够解决大数据环境下的信息过载问题,成为社交网络、电子商务、音乐点播等WEB2.0服务的核心技术[1, 2]。协同过滤是推荐系统中一种热门的推荐技术,其基本思想是根据用户过去的浏览记录、购买记录、评分记录及其主页标注等信息,分析用户潜在的兴趣偏好,以给用户提供个性化的推荐服务。因而,收集的用户信息越多,利用协同过滤产生的推荐结果越好。然而,现实中用户在项目上的评分数据极端稀疏,造成推荐质量低下的问题[3, 4]。
为降低数据稀疏性对系统推荐质量的影响,传统的协同过滤算法常常采用相关相似性[5]和余弦相似性[6]2种度量方法计算用户间的相似度。然而,传统的相似性度量方法仅仅考虑了用户间共同评分项的评分信息,使得为目标用户找到近邻的准确性和可靠性难以得到保证。针对上述问题,许多研究人员相继提出了新的相似性度量方法以改善系统对稀疏数据的处理能力。其中,文献[7]利用sigmoid函数对相关相似性方法做了较大改进,所提SPCC(sigmoid function based Pearson correlation coefficient)方法突出了共同评分项数量对刻画用户之间关系的重要性,用户之间的共同评分项越多,sigmoid函数值越大,用户间的相似度相对更大。由于余弦相似性方法中没有考虑到用户的评分尺度,文献[8]提出一种改进的余弦相似性度量方法ACOS(Adjusted cosine)。文献[9]提出了一种适用于解决冷启动问题[10]的相似性度量方法PIP(proximity,impact,and popularity),该方法虽然充分考虑了用户间共同评分项的近似度、影响度及流行度3个因素,但是局限于在局部考虑用户相似性。在PIP方法的基础上,文献[11]提出了一种基于新启发式的相似模型(new heuristic similarity model,NHSM),保留了PIP方法的优点,而且在整体上考虑了用户间的共同评分项数量和用户的评分倾向性,并将三者的乘积作为计算用户间相似度的标准。另外,一些研究人员提出了改进的近邻选择方法以提高推荐质量。文献[12]提出了一种改进的SlopeOne算法,该算法通过同时考虑用户的评分行为和用户环境以更好的度量用户间的相似性大小。文献[13]根据项目间的相似性对未评分项填补评分数据,然后根据用户间的相似性大小获取目标用户的近邻集合。文献[14]不仅考虑了用户间的相似性大小,也考虑了用户所处群体间的相似性大小。文献[15]利用用户的信用等级来代替用户间相似度的计算,更好地刻画了用户间的相似性大小。文献[16]分别定义了用户间局部相似性度量和全局度量方法,然后结合二者获得未评分项的预测值。文献[17]提出了通用近邻的概念,这些通用近邻可以作为所有目标用户的近邻。
尽管研究人员从不同角度提出了多种改进方法[18, 19, 20, 21],并取得了不错的效果,但是用户关系的准确刻画仍是提高推荐质量的关键。据此,本研究提出了一种基于信息熵的协同过滤算法。首先,利用相关相似性方法计算用户间的相似度以建立用户间的相似度矩阵;其次,计算所有用户的信息熵。根据用户信息熵的大小,将用户划分到两个不同的用户群体;然后,利用大间隔的方法得到目标用户与其他用户的间隔距离,利用计算得到的间隔距离和目标用户的信息熵,确定目标用户的近邻选择范围;接下来,判断用户信息熵是否在近邻选择范围之内,若不存在,则在相似度矩阵中修正该用户和目标用户的相似性大小;最后,得到用户的信息熵和与目标用户的相似度均满足要求的近邻集合。试验结果表明,基于信息熵的协同过滤算法能有效地提高系统推荐质量。该算法充分利用了少量数据所提供的信息,综合考虑了用户信息熵、用户的评分倾向、用户间的评分差异及共同评分项等众多影响因素,能够显著地提高预测质量。
1 预备知识在推荐系统中,用户对项目的评分数据可用一个m×n的评分矩阵R表示,该评分矩阵包含m个用户的集合User={U1,U2,…,Um}和n个项目的集合Item={I1,I2,…,In},如表1所示。其中,矩阵的行表示用户(1≤i≤m),列表示项目(1≤j≤n),Ri,j表示用户Ui在项目Ij上的评分。
| 表1 用户项目评分矩阵 Table 1 User-item rating matrix |
传统基于用户的推荐模型核心在于获取目标用户的近邻,而近邻的搜寻取决于用户间的相似性大小。常用的相似性度量方法如下。
(1) 相关相似性(Pearson correlation coefficient,PCC):用户间的相似度通过皮尔逊相关系数度量。
$sim\left( {{U}_{a}},{{U}_{a}} \right)=\frac{\sum\limits_{k\in \left( {{U}_{a}},{{U}_{a}} \right)}^{{}}{\left( {{R}_{a,k}}-{{{\bar{R}}}_{a}} \right)}\times \sum\limits_{k\in \left( {{U}_{a}},{{U}_{a}} \right)}^{{}}{\left( {{R}_{b,k}}-{{{\bar{R}}}_{b}} \right)}}{\sqrt{\sum\limits_{k\in \left( {{U}_{a}},{{U}_{a}} \right)}^{{}}{{{\left( {{R}_{a,k}}-{{{\bar{R}}}_{a}} \right)}^{2}}}}\times \sqrt{\sum\limits_{k\in \left( {{U}_{a}},{{U}_{a}} \right)}^{{}}{{{\left( {{R}_{b,k}}-{{{\bar{R}}}_{b}} \right)}^{2}}}}}$
(1)
(2) 余弦相似性(Cosine,COS):把每个用户的所有评分记录看成一个向量,用户间的相似度通过向量间的余弦夹角度量。
$sim\left( {{U}_{a}},{{U}_{a}} \right)=\frac{\sum\limits_{k\in \left( {{U}_{a}},{{U}_{a}} \right)}^{{}}{R_{a,k}^{2}}\times {{R}_{b,k}}}{\sqrt{\sum\limits_{k\in \left( {{U}_{a}},{{U}_{a}} \right)}^{{}}{R_{a,k}^{2}}}\times \sqrt{\sum\limits_{k\in \left( {{U}_{a}},{{U}_{a}} \right)}^{{}}{R_{b,k}^{2}}}}$
(2)
在公式(1)、(2)中,sim(Ua,Ub)表示用户Ua和Ub的相似度; c(Ua,Ub)表示用户Ua和Ub共同评分项的集合;${{{\bar{R}}}_{a}}$表示用户Ua已评分项的平均评分。
计算相似性大小可以得到用户间的相似度矩阵,记为sim。从sim中找到与目标用户相似度较大的前k个用户组成目标用户的近邻集合。最后,利用近邻集合预测目标用户的未评分项,预测公式为
${{P}_{t.i}}={{{\bar{R}}}_{t}}\frac{\sum\limits_{x=1}^{k}{sim\left( {{U}_{t}},{{U}_{x}} \right)\times \left( {{R}_{x,i}}-{{{\bar{R}}}_{x}} \right)}}{\sum\limits_{x=1}^{k}{\left| sim\left( {{U}_{t}},{{U}_{x}} \right) \right|}},$
(3)
假设X为一个离散的随机变量,其取值范围为{x1,x2,…xn},P是X上值的概率分布函数。信息熵的计算公式[22]为
H(X)=-$\sum\limits_{q=1}^{n}{{}}$P(xq)log P(xq)。
(4)
若P(x1)=P(x2)=…=P(xn),H(X)取得最大值;若P(xq)=1,H(X)取得最小值。
1.3 大间隔
给定一个样本集合{X1,X2,…,Xm},Xi为其中的一个样本,则样本Xi假设间隔的计算公式[23]为
θ(Xi)=$\frac{1}{2}$(║Xi-nearmiss(Xi)║-║Xi-nearhit(Xi)║),
(5)
传统基于用户的推荐模型本质上是利用用户的评分信息刻画用户之间的相似性,与目标用户相似程度高的用户被选中作为预测未评分项的近邻。然而,由于用户的评分数据极端稀疏,用户间的共同评分项数量极少,传统的相似度计算对于刻画用户之间的相似性缺乏可信度。另外,传统的相似性度量方法没有考虑目标用户与其近邻的评分倾向。基于此,结合用户的信息熵和用户间的相似性大小,提出了一种基于信息熵的协同过滤算法。
2.1 基于信息熵的间隔距离度量定义 1[24] 假设用户的评分范围是一个离散的评分集合{x1,x2,…,xn},xq为其中一个评分(1≤q≤n),则用户Ui上xq的概率分布函数P(xq)等于评分为xq的项目个数占用户Ui已评分项总个数的比率。用户Ui的信息熵
| H(Ui)=-$\sum\limits_{q={{x}_{1}}}^{{{x}_{n}}}{{}}$ | (6) |
针对用户评分的倾向性,即:有的用户倾向打高分,有的用户倾向打低分及有的用户会根据自身的兴趣偏好对不同的项目给出区别度较大的评分,通过计算用户的信息熵可以区分有不同评分偏好的用户,用户的信息熵直接反映了用户对项目评分的分布情况,从侧面也反映出用户的评分倾向程度。然而,评分分布相似的用户信息熵相近,特别地,倾向打高分的用户和倾向打低分的用户信息熵相近。
例 1 给定一个实际的评分矩阵,如表2所示。其中,矩阵的行表示用户,列表示项目。
| 表2 实际评分矩阵 Table 2 Actual rating matrix |
根据公式(6)可得用户U1和U3的信息熵为1,用户U2和U4信息熵为1.585。然而,从表2中可看出,U1对项目的的评分偏高,U3则倾向打低分。尽管U1和U3的信息熵相同,却存在完全不同的评分倾向。针对上述问题,为了在整体上把握用户的评分倾向,在考虑用户信息熵的同时,也须考虑用户间的评分差异。为了反映用户间的评分差异,采用PCC方法计算用户间的相似性大小。
至此,根据用户间信息熵的差异,评分区别度大的用户可以很好的与倾向性明显的用户区分开来。针对倾向打高分的用户和倾向打低分的用户,由于评分分布相似,因而,单考虑用户的信息熵难以区分两者,需要结合用户间的相似性大小。若二个用户的评分差异同样接近,则这两个用户很有可能互为近邻,反之,两个用户不相似。从而,目标用户能够获取与其有相似评分分布和相同评分倾向的近邻。为了将用户信息熵用于协同推荐,设计了一种基于大间隔的距离度量方法。首先,根据用户信息熵将用户划分到不同的用户群体。
定义 2 给定两个用户群体,记为HG和LG。若用户Ui的信息熵H(Ui)≥δ,Ui∈HG;若H(Ui)<δ,Ui∈LG。其中,阈值δ的计算公式为
δ=$\frac{\sum\limits_{i=1}^{m}{H\left( {{U}_{i}} \right)}}{m},$
(7)
在定义2中,根据用户的信息熵,用户被划分到不同的用户群体,增加了用户间的区分度,以便利用大间隔方法得到目标用户与其他用户的间隔距离。
例 2 在表2中,根据公式(6)可得δ=1.292 5。根据定义2,用户U1和U3被划分到用户群体HG中,用户U2和U4被划分到用户群体LG中。
定义 3 给定用户Ut和Ua,其中Ut为目标用户。若H(Ut)≥δ,目标用户Ut与其他用户Ua的间隔距离
θ(Ut,Ua)=$\frac{1}{2}$(H(Ut)-$\underset{{{U}_{a}}\in LG}{\mathop{\max }}\,$-$\underset{{{U}_{a}}\in HG}{\mathop{\min }}\,$|H(Ut)-H(Ua)|)。
(8)
若H(Ua)<δ,目标用户Ut与其他用户Ua的间隔距离
θ(Ut,Ua)=$\underset{{{U}_{a}}\in HG}{\mathop{\min }}\,$H(Ua)-H(Ut)-$\underset{{{U}_{a}}\in LG}{\mathop{\min }}\,$|H(Ut)-H(Ua)|)。
(9)
基于大间隔的距离度量方法通过设计一种新的距离度量公式,使得目标用户与其近邻有一致的评分倾向,而与目标用户评分倾向不同的用户则避免成为其近邻。在定义3中,该方法体现了用户间信息熵的差异,能够将与目标用户信息熵相差较大的用户分隔开,便于为目标用户找到准确可靠的近邻。接下来,根据目标用户与其他用户的间隔距离及其信息熵,可以得到目标用户的近邻选择范围。
定义 4 假设目标用户Ut与其他用户Ua的间隔距离为θ(Ut,Ua),目标用户的信息熵为H(Ut)。若用户Ub为目标用户Ut的近邻,则:用户Ub的信息熵H(Ub)应满足
| H(Ut)-α×θ(Ut,Ua)≤H(Ub)≤H(Ut)+α×θ(Ut,Ua)。 |
在定义4中,与目标用户信息熵相差较大的用户被排除在近邻选择范围之外,降低了推荐结果的偶然性。同时,考虑到用户的评分数据极端稀疏,用于计算用户间相似度和推荐给目标用户的数据有限,而且不同数据集上评分矩阵的结构存在差异。因而,通过设置一个阈值α以调节用户信息熵对推荐结果的影响,使得在可用数据稀疏的情况下,最大程度上提高所选目标用户近邻的质量。
例 3 假设目标用户Ut与其他用户Ua的间隔距离θ(Ut,Ua)=0.8,H(Ut)=1.35,阈值α=1.0,则目标用户Ut的近邻选择范围为[0.55,2.15]。
2.2 基于信息熵的协同过滤模型
通过第2.1节的分析可知,基于信息熵的协同过滤算法主要分为4个步骤:第一步,计算用户间的相似度得到用户间的相似度矩阵,记为sim;第二步,根据目标用户与其他用户的间隔距离及其信息熵,得到该目标用户的近邻选择范围;第三步,判断目标用户与其他用户的关系。若用户的信息熵不在近邻选择范围内,则该用户与目标用户不存在相似关系,在矩阵sim中修正该用户与目标用户的相似度,反之,sim中该用户与目标用户的相似度保持不变。修正之后的相似度矩阵记为newsim。最后,根据矩阵newsim中用户间的相似性大小,搜寻目标用户的近邻,并产生推荐结果:
${{P}_{t.i}}={{{\bar{R}}}_{t}}\frac{\sum\limits_{x=1}^{k}{newsim\left( {{U}_{t}},{{U}_{x}} \right)\times \left( {{R}_{x,i}}-{{{\bar{R}}}_{x}} \right)}}{\sum\limits_{x=1}^{k}{\left| newsim\left( {{U}_{t}},{{U}_{x}} \right) \right|}},$
(10)
根据上述描述,设计算法如下:
算法: 基于信息熵的协同过滤推荐算法(Entropy-based-CF)
输入: 用户-项目评分矩阵R,阈值α;
输出: 目标用户Ut在未评分项上的预测评分Pt,i。
步骤 1 通过公式(1),利用PCC方法计算用户间的相似性大小,得到用户间的相似度矩阵,记为sim;
步骤 2 通过公式(6),计算所有用户的信息熵;
步骤 3 利用公式(7)计算阈值δ,然后根据定义2将用户逐一划分到用户群体HG或LG中;
步骤 4 根据定义3计算目标用户Ut与其他用户Ua的间隔距离;
步骤 5 根据定义4得到Ut的近邻选择范围;
步骤 6 若用户的信息熵在近邻选择范围之外,则在矩阵sim中修正该用户和Ut的相似性大小,其值改为-1;反之,sim中该用户和Ut的相似度保留原来的值。修正以后得到新的相似度矩阵,记为newsim;
步骤 7 根据矩阵newsim中用户间的相似性大小得到Ut的近邻集合;
步骤 8 利用公式(10),预测Ut在未评分项Ii上的评分Pt,i。
3 试验结果及分析试验从2个方面展开:一是通过改变阈值α的取值,分析基于信息熵的协同过滤算法对推荐结果的影响;二是比较所提算法与其他协同过滤算法的推荐质量。
3.1 数据集选用公开的MovieLens数据集(ML数据集)和HetRec2011-MovieLens数据集(HML数据集)对算法有效性进行验证(数据集可在http://www.grouplens.org/下载)。其中,ML数据集包含943个用户在1 682个电影上的100 000条评分记录,每个用户至少有20条评分记录,评分范围为1~5,评分矩阵的稀疏等级为0.937 0。鉴于HML数据集中评分记录过多,随机选择了其中的404个用户在1 300个电影上的39 259条评分记录,每个用户至少有3条评分记录,评分范围为1~5,评分矩阵的稀疏等级为0.925 4。另外,为了便于计算用户信息熵,将类似0.5,1.5的评分记录取整,如用户对电影的评分为3.5,将评分转换为4,该转换并未造成信息丢失。另外,为了保证试验结果的无偏性,整个试验采用5折交叉验证。数据集分为测试集和训练集2个部分,测试集占数据集的20%,余下80%的数据作为训练集。测试集之间是互斥的,并有效地覆盖整个数据集。
3.2 度量指标试验采用平均绝对偏差MAE(mean absolute error)和覆盖率Coverage作为度量算法优劣程度的标准。MAE是通过计算预测的用户评分和实际用户评分之间的偏差以评价预测结果的准确性,MAE值越小,算法的预测质量越高。Coverage用来衡量一个算法能够预测的项目占所有项目的百分比,Coverage值越大,算法的全面性越好。
假设用户在n个项目有评分,用户实际评分的集合记为r={r1,r2,…,rn},对应预测的用户评分集合记为p={p1,p2,…,pn},s表示集合p中的评分个数。度量指标MAE和Coverage的计算公式分别表示为:
| $MAE=\frac{\sum\limits_{k=1}^{n}{\left| {{p}_{i}}-{{r}_{i}} \right|}}{n},\operatorname{cov}=\frac{s}{n}.$ |
为了反映阈值α对推荐结果的影响,选取不同的α值以观测不同数据集上MAE的变化情况,如表3所示。在ML数据集上α值分别取0.5,1.0和1.5。当近邻数k取较小的值时(如k取10和20),随着阈值α越来越小,MAE值也越来越小;当近邻数k较多时(如k取90和100),随着阈值α越来越小,MAE值逐渐增大。可以看出,利用用户的信息熵反映用户的评分偏好,有利于提高推荐结果的准确率。当α取较小值时,目标用户能够找到与其信息熵足够接近且相似度高的用户作为其近邻,显著地提高了推荐质量。然而,α值过小导致与目标用户的信息熵之差较大的用户排除在近邻选择范围之外,加剧了数据的稀疏程度,使得k取较大值时推荐结果的误差反而升高了。实质上,α取较小值(如α=0.5)加强了用户的信息熵对推荐结果的影响;α取较大值(如α=1.5)则弱化了信息熵的作用,用户间的相似性大小对推荐结果的作用变大。为了平衡用户的信息熵与用户间的相似度对推荐结果的影响,通过取步长0.5重复试验,对于ML数据集,在后续的试验中设置α=1.0。
在HML数据集中,当α=1.0时,随着近邻数k的不断增加,推荐质量提升的空间越来越小,与ML数据集中α=0.5的情况类似。因此,对比ML数据集,可以通过增大阈值α以提高算法在近邻数k较多时的推荐质量。从表3中可以看出,α分别取1.0,4.0和8.0时,所提算法在HML数据集上MAE值的变化情况与ML数据集中α分别取0.5,1.0和1.5时的变化规律一致。对于HML数据集,在后续的试验中α=4.0。
| 表3 阈值α的影响 Table 3 The effect of threshold value α |
为了进一步验证所提算法的有效性,2种传统的推荐算法和2种较新的推荐算法被选作比较对象:基于PCC的协同过滤算法(PCC-CF)[5],基于Cosine的协同过滤算法(COS-CF)[6],基于SPCC的协同过滤算法(SPCC-CF)[7]及基于NHSM的的协同过滤算法(NHSM-CF)[10]。近邻数k的取值为10~100。
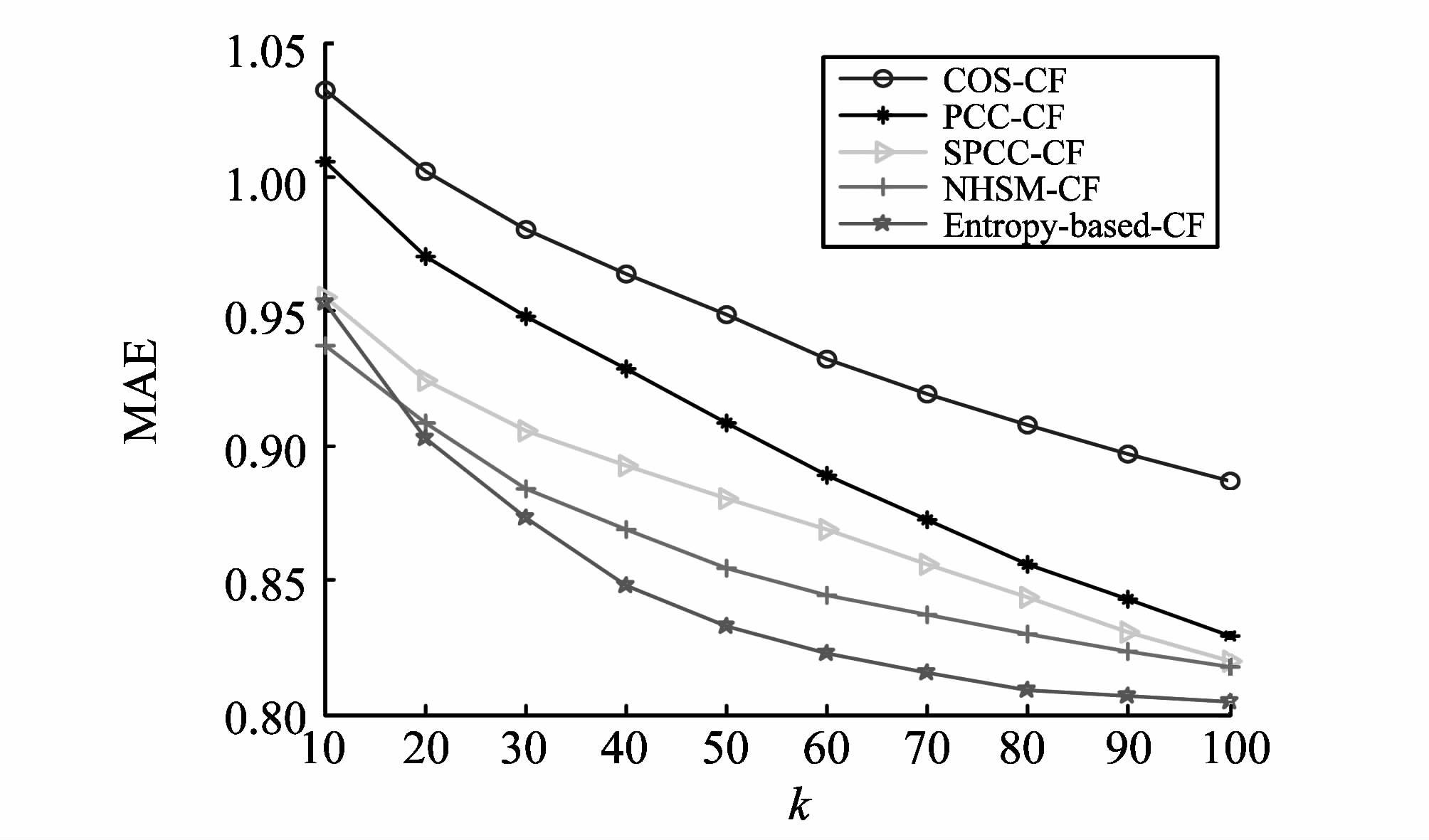
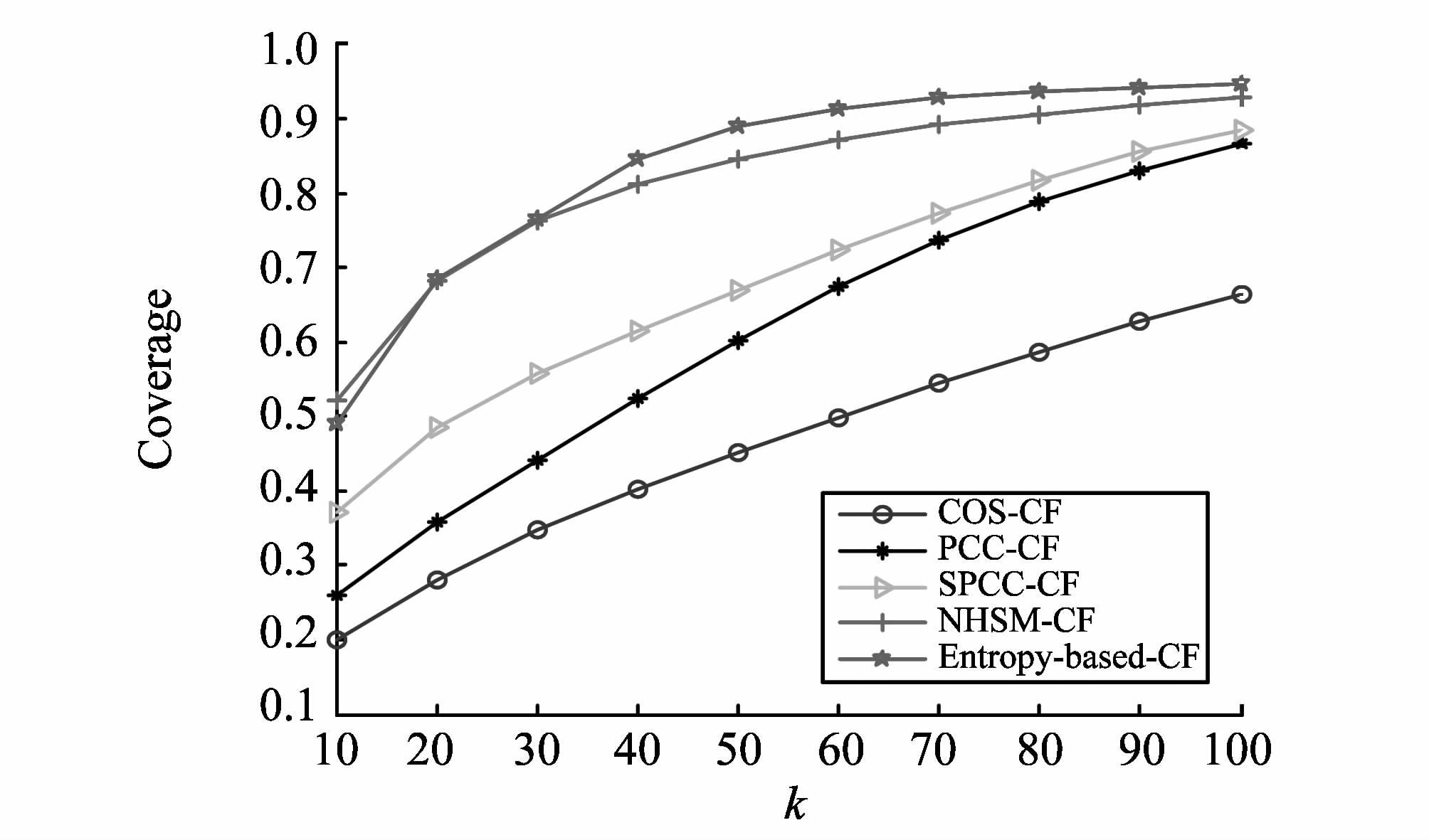
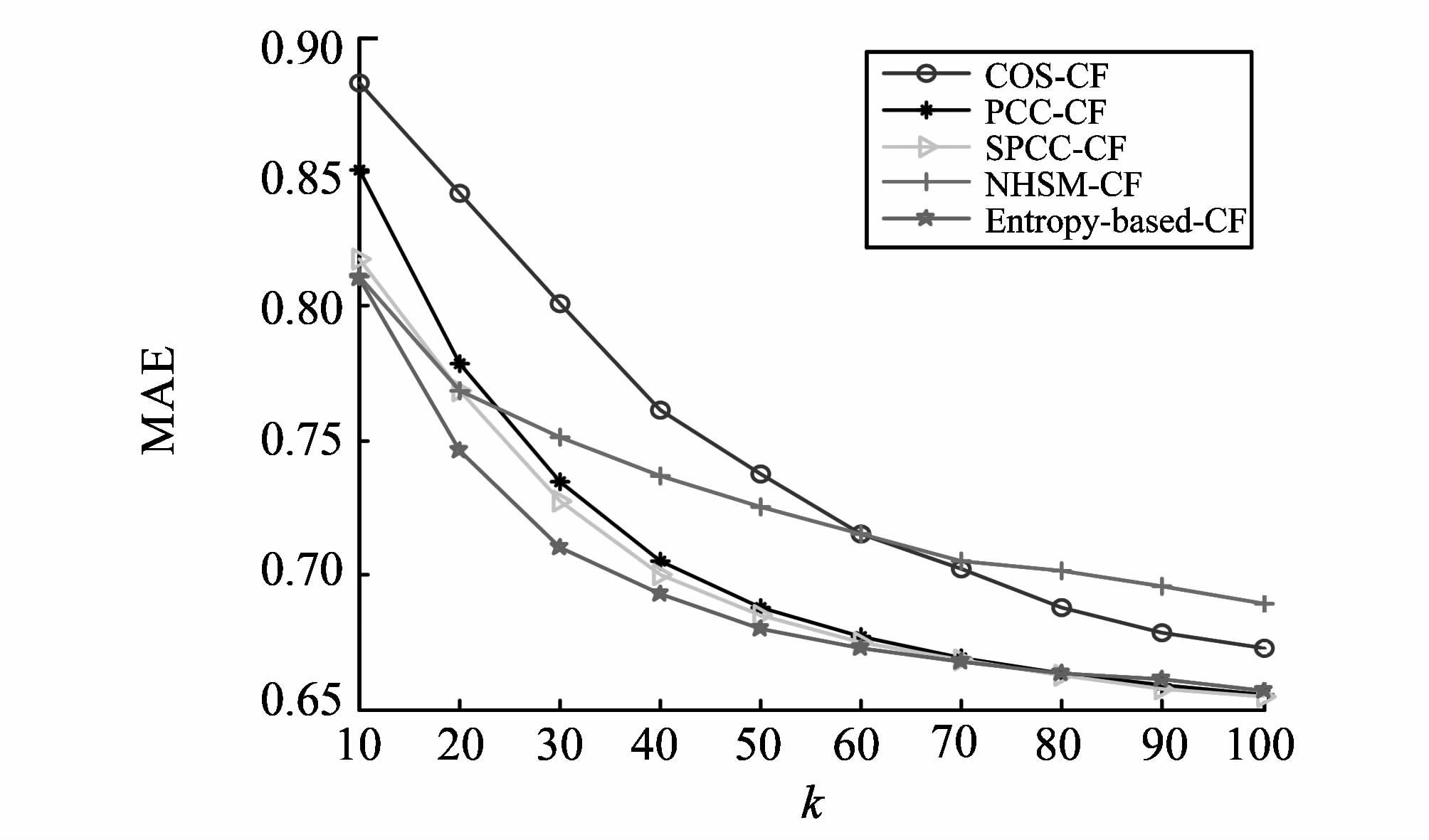
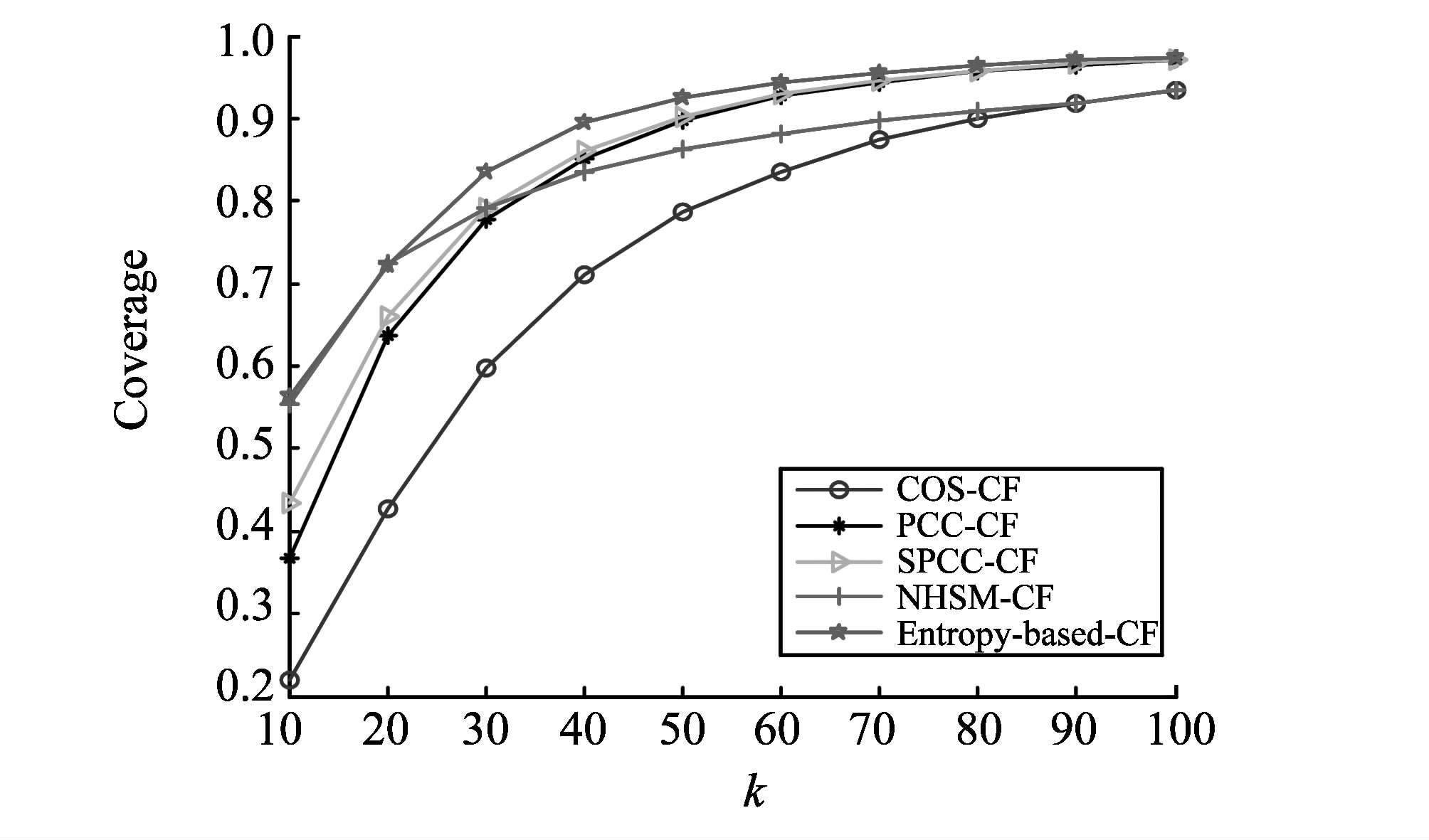
图1和图2分别展示了ML数据集上不同算法MAE和Coverage的变化情况。可以看出,随着近邻数k逐渐增加,相比其他推荐算法,所提算法在整体上能得到更小的MAE值和更大的Coverage值。其中,当k=10时,NHSM-CF的推荐质量在所有算法中最好。然而,根据第3.3.1节的分析可知,通过降低阈值α可以提高所提算法在近邻数k较少时的预测质量,以表3中α=0.5为例,所提算法在k=10时得到的MAE值为0.939 2,这与NHSM-CF得到的结果非常接近。HML数据集上不同算法MAE和Coverage的变化情况分别如图3和图4所示。可以看出,HML数据集上MAE和Coverage的变化情况和ML数据集类似,所提算法的推荐性能在各项指标中均占优。据此可知,基于信息熵的协同过滤算法能够有效地提高推荐质量。
|
图1 ML数据集上的MAE Fig.1 The MAE based on ML data set |
|
图2 ML数据集上的Coverage Fig.2 The Coverage based on ML data set |
|
图3 HML数据集上的MAE Fig.3 The MAE based on HML data set |
|
图4 HML数据集上的Coverage Fig.4 The Coverage based on HML data set |
在信息过载的大环境下为用户推荐有价值的信息,受到越来越广泛的关注。协同过滤作为推荐系统中成功的推荐技术之一,有利于为用户提供更加优质的个性化推荐服务。然而,由于现实中评分数据的稀疏性,推荐结果无法令用户满意。受信息熵的启发,在传统基于用户的推荐模型上进一步提出了基于信息熵的协同过滤算法。所提算法不仅保留了传统算法的优势,即:充分利用了用户间共同评分项的评分信息,而且设计了一种基于信息熵的近邻选择方法,充分考虑了用户评分偏好等多个影响因素。试验结果表明,设置适当的阈值,算法的推荐质量有较大提高。
| [1] | ADOMAVICIUS G, TUZHILIN A. Toward the next generation of recommender systems:a survey of the state-of-the-art and possible extensions[J]. IEEE Transactions on Knowledge and Data Engineering, 2005, 17(6):734-749.( 1) 1) |
| [2] | LI Yanen, ZHAI Chengxiang, Chen Ye. Exploiting rich user information for one-class collaborative filtering[J]. Knowledge and Information Systems, 2014, 38(2):277-301.( 1) 1) |
| [3] | SHI Yue, LARSON M, HANJALIC A. Collaborative filtering beyond the user-item matrix:a survey of the state of the art and future challenges[J]. ACM Computing Surveys, 2014, 47(1):3:1-3:45.( 1) 1) |
| [4] | BOBADILLA J, ORTEGA F, HEMANDO A, et al. Recommender systems survey[J]. Knowledge-Based Systems, 2013, (46):109-132.( 1) 1) |
| [5] | BREESE J S, HECKERMAN D, KADIE C. Empirical Analysis of Predictive Algorithms for Collaborative Filtering[C]//Proceedings of the 14th Conference on Uncertainty in Artificial Intelligence. Madison, USA:UAI, 1998:43-52.( 2) 2) |
| [6] | RESNICK P, IACOVOU N, SUCHAK M, et al. GroupLens:An open architecture for collaborative filtering of netnews[C]//Proceedings of the ACM Conference on Computer Supported Cooperative Work. Chapel Hill, USA:ACM, 1994:175-186.( 2) 2) |
| [7] | JAMALI M, ESTER M. TrustWalker:a random walk model for combining trust-based and item-based recommendation[C]//Proceedings of the 15th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York, USA:ACM, 2009:397-406.( 2) 2) |
| [8] | SARWAR B, KARPIS G, KONSTAN J, et al. Item-based collaborative filtering recommendation algorithms[C]//Proceedings of the 10th International Conference on World Wide Web. New York, USA:ACM, 2001:285-295.( 1) 1) |
| [9] | AHN H J. A new similarity measure for collaborative filtering to alleviate the new user cold-starting problem[J]. Information Sciences, 2008, 178(1):37-51.( 1) 1) |
| [10] | 李改,李磊.一种解决协同过滤系统冷启动问题的新算法[J].山东大学学报(工学版),2012,42(2):11-17. LI Gai, LI Lei. A new algorithm of cold-start in a collaborative filtering system[J]. Journal of Shandong University(Engineering Science), 2012, 42(2):11-17.(  2) 2) |
| [11] | LIU Haifeng, HU Zheng, MIAN Ahmad, et al. A new user similarity model to improve the accuracy of collaborative filtering[J]. Knowledge-Based Systems, 2014(56):156-166.( 1) 1) |
| [12] | 邓晓懿,金淳,韩庆平,等.基于情境聚类和用户评级的协同过滤推荐模型[J].系统工程理论与实践,2013,33(11):2945-2953. DENG Xiaoyi, JIN Chun, HAN Qingping, et al. Improved collaborative filtering model based on context clustering and user raking[J]. Systems Engineering—Theory & Practice, 2013, 33(11):2945-2953.(  1) 1) |
| [13] | 邓爱林,朱扬勇,施伯乐.基于项目评分预测的协同过滤推荐算法[J].软件学报,2003,14(9):1621-1628. DENG Ailin, ZHU Yangyong, SHI Bole. A collaborative filtering recommendation algorithm based on item rating prediction[J]. Journal of Software, 2003, 14(9):1621-1628.(  1) 1) |
| [14] | 林耀进,胡学钢,李慧宗.基于用户群体影响的协同过滤推荐算法[J].情报学报,2013,32(3):299-305. LIN Yaojin, HU Xuegang, LI Huizong. Collaborative filtering recommendation algorithm based on user group influence[J]. Journal of the China Society for Scientific and Technical Information, 2013, 32(3):299-305.(  1) 1) |
| [15] | JEONG B, LEE J, CHO H. User credit-based collaborative filtering[J]. Expert Systems with Applications, 2009, 36(6):7309-7312.( 1) 1) |
| [16] | ANAND D, BHARADWAJ K K. Utilizing various sparsity measures for enhancing accuracy of collaborative recommender systems based on local and global similarities[J]. Expert Systems with Applications, 2011, 38 (5):5101-5109.( 1) 1) |
| [17] | BOUMAZA A, BRUN A. Stochastic search for global neighbors selection in collaborative filtering[C]//Proceedings of the 27th Annual ACM Symposium on Applied Computing. New York, USA:ACM, 2012:232-237.( 1) 1) |
| [18] | 黄创光,印鉴,汪静,等.不确定近邻的协同过滤推荐算法[J].计算机学报,2010,33(8):1369-1377. HUANG Chuangguang, YIN Jian, WANG Jing, et al. Uncertain neighbors′ collaborative filtering recommendation algorithm[J]. Chinese Journal of Computers, 2010, 33(8):1369-1377.(  1) 1) |
| [19] | 李聪,梁昌勇,马丽.基于领域最近邻的协同过滤推荐算法[J].计算机研究与发展,2008,45(9):1532-1538. LI Cong, LIANG Changyong, MA Li. A collaborative filtering recommendation algorithm based on domain nearest neighbor[J]. Journal of Computer Research and Development, 2008, 45(9):1532-1538.(  1) 1) |
| [20] | LIU Qi, CHEN Enhong, XIONG Hui, et al. Enhancing collaborative filtering by user interest expansion via personalized ranking[J]. IEEE Transactions on Systems, Man, and Cybernetics, 2012, 42(1):218-233.( 1) 1) |
| [21] | BOBADILLA J, HERNANDO A, ORTEGA F, et al. Collaborative filtering based on significances[J]. Information Sciences, 2012, 185(1):1-17.( 1) 1) |
| [22] | LIN Yaojin, HU Xuegang, WU Xindong. Quality of information-Based source assessment and selection[J]. Neurocomputing, 2014(133):95-102.( 1) 1) |
| [23] | YANG Ming, WANG Fei, YANG Ping. A novel feature selection algorithm based on hypothesis-margin[J]. Journal of Computers, 2008, 3(12):27-34.( 1) 1) |
| [24] | KALELI C.An entropy-based neighbor selection approach for collaborative filtering[J]. Knowledge-Based Systems, 2014(56):273-280.( 1) 1) |



