2. 郑州航空工业管理学院土木建筑工程学院, 河南 郑州 450015
2. Institute of Civil Engineering and Architecture, Zhengzhou Institute of Aeronautical Industry Management,Zhengzhou 450015, Henan, China
应力监测方法是近年来兴起的、较为新颖的岩质边坡监测预警方法,与位移监测相比,该方法具有应力变化超前于位移、监测易于操作、数据波动小的优势,其工程实用性值得进行深入研究。由于边坡失稳是我们所不愿看到的灾害,所以如何获取应力变化规律变得尤为重要。因此,本研究借助离心模型试验方法,离心模型试验可以通过提高离心加速度重现边坡在自重作用下的失稳过程[1, 2, 3, 4, 5, 6, 7],可以对边坡的变形以及支护结构的受力进行监测,是研究岩质边坡破坏过程中的位移和应力变化规律的较为先进的试验手段。
由于仪器设备的局限性,采用模型试验,特别是离心模型试验的方法对岩质边坡失稳过程的监测问题进行研究历时较短。STEWART D P等利用离心模型试验研究了岩质边坡的倾倒破坏,表明采用离心模型试验研究岩质边坡失稳具有可行性[8];陈祖煜等利用离心模型试验机,将锚固系统施加到岩质边坡中,得出岩质边坡的倾倒破坏滑动面呈双折线型,并绘制了边坡失稳前岩体监测锚杆(索)的应力变化与离心加速度的实时曲线[9, 10, 11, 12];邓卫东等采用碎石加泥浆胶结的方式模拟完全碎裂型路堑岩质边坡,得出该类边坡的破坏形式为追踪台阶破坏,地质模型为滑移-压致拉裂机制[13];唐红梅等在模型试验中以 硼砂、水、砂、水泥、石膏为原料模拟边坡岩体,研究表明:与应力监测相比,岩质边坡应力监测易于把握,并提出应以三维应力监测为主、位移监测为辅的边坡监测方案[14];冯振等通过离心模型试验重现了斜倾厚层岩质边坡的“后部块体驱动——前缘关键块体瞬时失稳”模式[15]。
本研究在已有研究成果的基础上,首次采用离心模型试验方法,对岩质边坡应力监测的可行性进行研究,并选取三类典型岩质边坡滑动破坏形式为例,对边坡破坏前的应力变化进行分析,得出应力变化规律和敏感监测部位,通过得出的数据拟合曲线为实际工程预警值确定提供参考。
1 边坡离心模型试验方案模型试验所采用的设备为TLJ-3型土工离心机,最大离心加速度为200g,最大容量为60g·t (g为重力加速度,t为吨),有效半径为2.0 m,模型箱长×宽×高=70 cm×50 cm×36 cm。
测试用全长粘结型锚杆替代材料应与实际锚杆的弹性模量E、锚杆直径相似。若根据相似比选择锚杆尺寸,锚杆的替代材料类似极细的铁丝,直径数量级约为10-2cm,除无法贴设测试元件外,还无法模拟锚杆与岩体的粘结效果。通过试验分析采用加工高刚度、高强度钢片(截面为矩形)替代锚杆,替代材料的抗拉弹性模量可以达到200 GPa左右,保持了与实际工程采用锚杆的弹性模量一致性。模型加工时预留注浆孔道,采用超细水泥浆作为锚杆粘结剂。
岩体替代材料应与实际岩体的弹性模量、重度、泊松比、粘聚力、内摩擦角、抗压强度相似[16, 17, 18, 19],离心试验的重点是确定模型材料的重力场相似[20],岩石力学参数在模型试验中并不能做到材料的完全相同,本研究以强风化砂岩为研究对象,考虑相似材料的弹性模量、抗剪强度、密度1∶1相似,根据相似条件采用重晶石粉、石英砂、石膏、水按照不同配比制备试样,试样质量比设为1.50∶1.00∶x∶0.50,其中以石膏作为胶结剂,石膏的含量决定了试样的强度。通过试验得出,岩石替代材料采用 m(重晶石粉)∶m(石英砂)∶m(石膏)∶m(水)=1.50∶1.00∶0.25∶0.50制备,替代材料的物理力学参数结果如表1所示,其中以石膏作为胶结剂。结构面处用拌合好的泥浆模拟,结构面抗剪强度为c=13 kPa,内摩擦角φ=19°,对未贯通的结构面采用厚塑料纸进行模拟。
| 表1 相似材料物理力学参数 Table 1 Physical and mechanical parameters of similarity material |
应力监测采用在锚杆表面贴设应变计监测锚杆受力变化的方法,由于离心机具有实时监控并传输数据的功能,可获得试验过程中锚杆的实时应变数据,这些数据反应出锚杆的应力,由于实际工程主要以轴力描述锚杆的受拉状态,所以通过换算式(1)得出原型锚杆轴力作为应力监测的判定值:
F=n2EεA,
(1)
试验共设计了3类典型岩质边坡的离心模型试验方案,分别为层状岩质边坡—分单平面滑动与顺层滑动、结构面控制岩质边坡、碎裂结构岩质边坡等对应力监测的应用状况进行研究。试验过程中通过观察监控仪器的数据突变和高清摄像相结合判断边坡是否失稳。
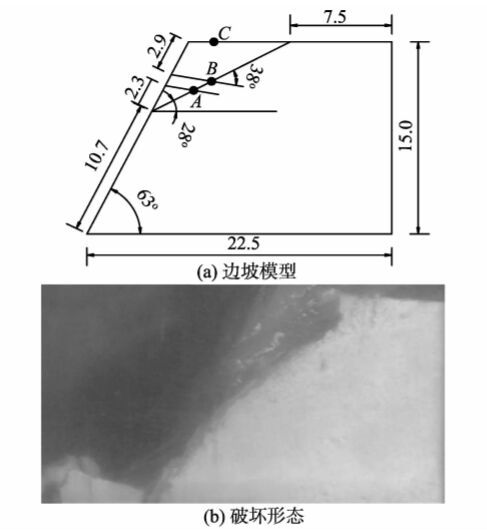
2 层状岩质边坡试验 2.1 单滑面滑动岩质边坡试验单滑面滑动岩质边坡是形式最为简单的层状岩质边坡,图1(a)为试验设计的单滑面滑动岩质边坡与监测形式,边坡高度为15 cm,坡度1.0∶0.5,应力监测分上下两个监测点,分别为A、B两处,A、B横向间距为5 cm。锚杆埋设角度与水平面夹角为10°。同时采用激光位移传感器对坡顶C点进行位移变形监测。通过增加离心加速度的形式使边坡达到极限平衡状态并失稳,同时利用离心机数据采集系统得出此过程中应力和位移的变化数据。
|
图1 单滑面岩质边坡模型 Fig.1 Rock slope model with single sliding surface |
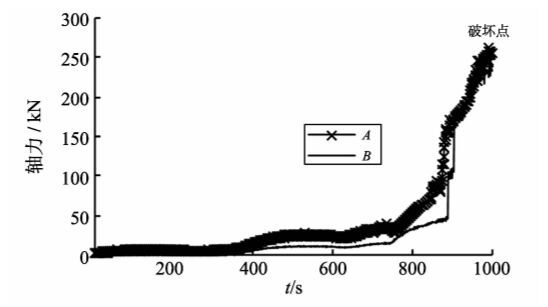
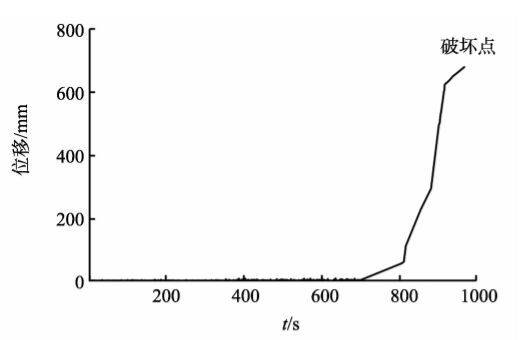
图1(b)中单滑面岩质边坡的破坏形式为沿结构面直线滑动。图2和图3为边坡运行时间内的轴力与时间关系曲线和位移与时间关系曲线,其中将监测位移与轴力还原为原型位移与轴力,可以得出锚杆轴力出现变化的时间要稍早于位移出现变化的时间,位移开始发生变化至破坏间隔300 s,而轴力开始变化至破坏间隔700 s,应力监测有更加充裕的时间对边坡是否失稳及失稳过程进行分析评判。试验结果表明边坡下滑力是一个不断增大的过程。当下滑力较小时,边坡并未出现位移,如果不进行应力监测无法得知此时边坡在积蓄下滑能量,当下滑力累计到一定数值时,边坡产生变形并突然失稳破坏。由此可见,应力监测的目的就是监测边坡下滑力不断累计增大的过程,在实际中应用是可行的。
|
图2 轴力-时间曲线 Fig.2 Curves of axial force and time |
|
图3 C点位移-时间曲线 Fig.3 Curves of displacement and time of point C |
由于本研究主要以应力监测的研究为主,后续模型试验中不再采用位移监测的方式。并重点分析锚杆轴力随离心加速度的变化规律。
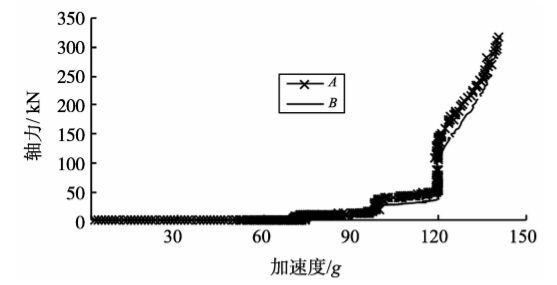
图4为锚杆轴力随加速度变化曲线,随着重力加速度的增加,边坡下滑力也逐渐加大,锚杆轴力也相应增加。A处轴力变化要稍敏感于B处,即下部监测要优于上部监测。
|
图4 锚杆轴力-加速度曲线 Fig.4 Curves of rock bolt axial force and acceleration |
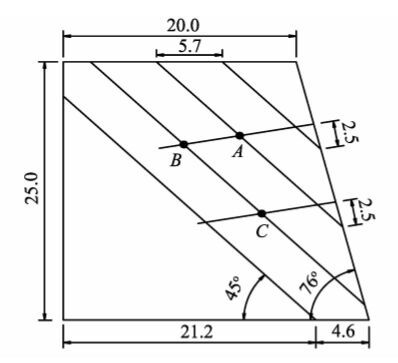
图5为试验设计的顺层岩质边坡与监测形式,边坡高度为25 cm,坡度1.00∶ 0.25,锚杆埋设角度与水平方向夹角为10°,应力监测点位为A、B、C三点。
|
图5 顺层岩质边坡模型 Fig.5 Bedding rock slope model |
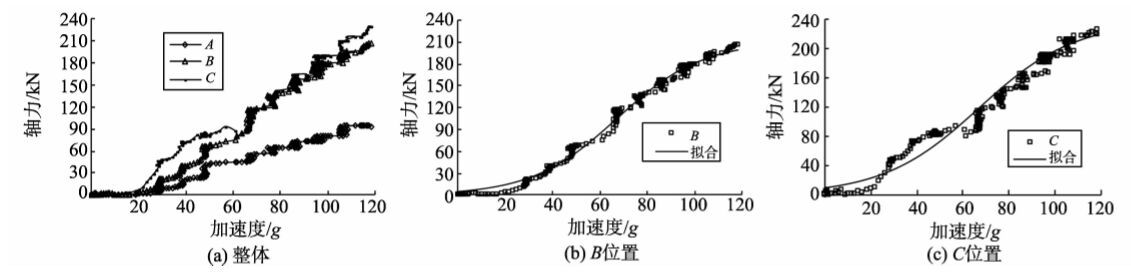
图6为锚杆轴力随离心加速度的变化曲线。应力监测结果显示,岩质边坡在离心加速度达到115.1 g时,边坡沿B、C点所在的结构面失稳破坏。C处轴力较大,应力变化要稍敏感于B处,二者相差不大,均可作为应力监测部位,以C位置较佳。由此可知,对于层状岩质边坡,整个滑动面均可作为应力监测的部位,但下部稍优于上部。其他监测位置,如A点,作为监测对比点,没有起到监测边坡的效果,受力很小,不具有监测的意义。由于边坡破坏过程在后期应力增长较快,对层状岩质边坡监测时,若采用人工监测,则需要增加监测点位和监测频率以确保监测预警及时有效。
|
图6 顺层岩质边坡锚杆轴力-加速度曲线 Fig.6 Curves of rock bolt axial force and acceleration of bedding rock slope |
根据曲线形态,采用Logistic曲线[21, 22, 23]对应力监测曲线图6(a)进行拟合,对曲线B进行拟合的结果如式(2)所示,相关系数为0.96;对曲线C拟合的结果如式(3)所示,相关系数为0.84,拟合曲线与原曲线的对比如图6(b)、图6(c)所示,两个主要监测点B、C处的轴力-加速度拟合公式相关系数较高,有很好的拟合效果。
$$y = {{236.4} \over {1 + {{\rm{e}}^{ - 0.048\left( {x - 67.066} \right)}}}},$$
(2)
$$y = {{211.1} \over {1 + {{\rm{e}}^{ - 0.0554\left( {x - 67.19} \right)}}}}$$
(3)
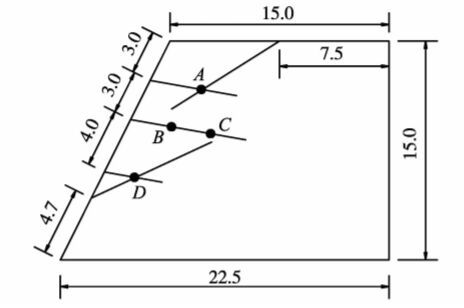
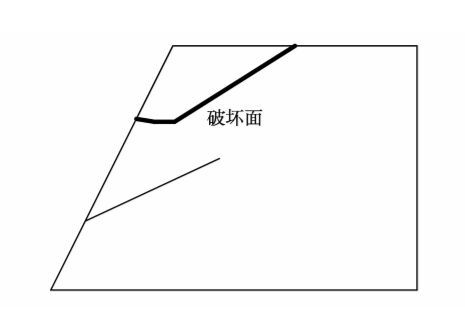
图7为试验设计的结构面控制岩质边坡与监测形式,边坡高度为15 cm,结构面以厚塑料纸替代,边坡坡度1.0∶0.5,结构面倾角30°,共布设3根监测锚杆,锚杆与水平面夹角为10°,监测4处点位。边坡破坏形式如图8所示,图中的滑动面与上部结构面有关,在结构面最靠近临空面位置处拉裂断开,重力加速度增大所产生的拉剪力是边坡失稳的主因。
|
图7 结构面控制岩质边坡模型 Fig.7 Rock slope model controlled by structure plane |
|
图8 结构面控制岩质边坡失稳图 Fig.8 Failure figure of rock slope controlled by structure plane |
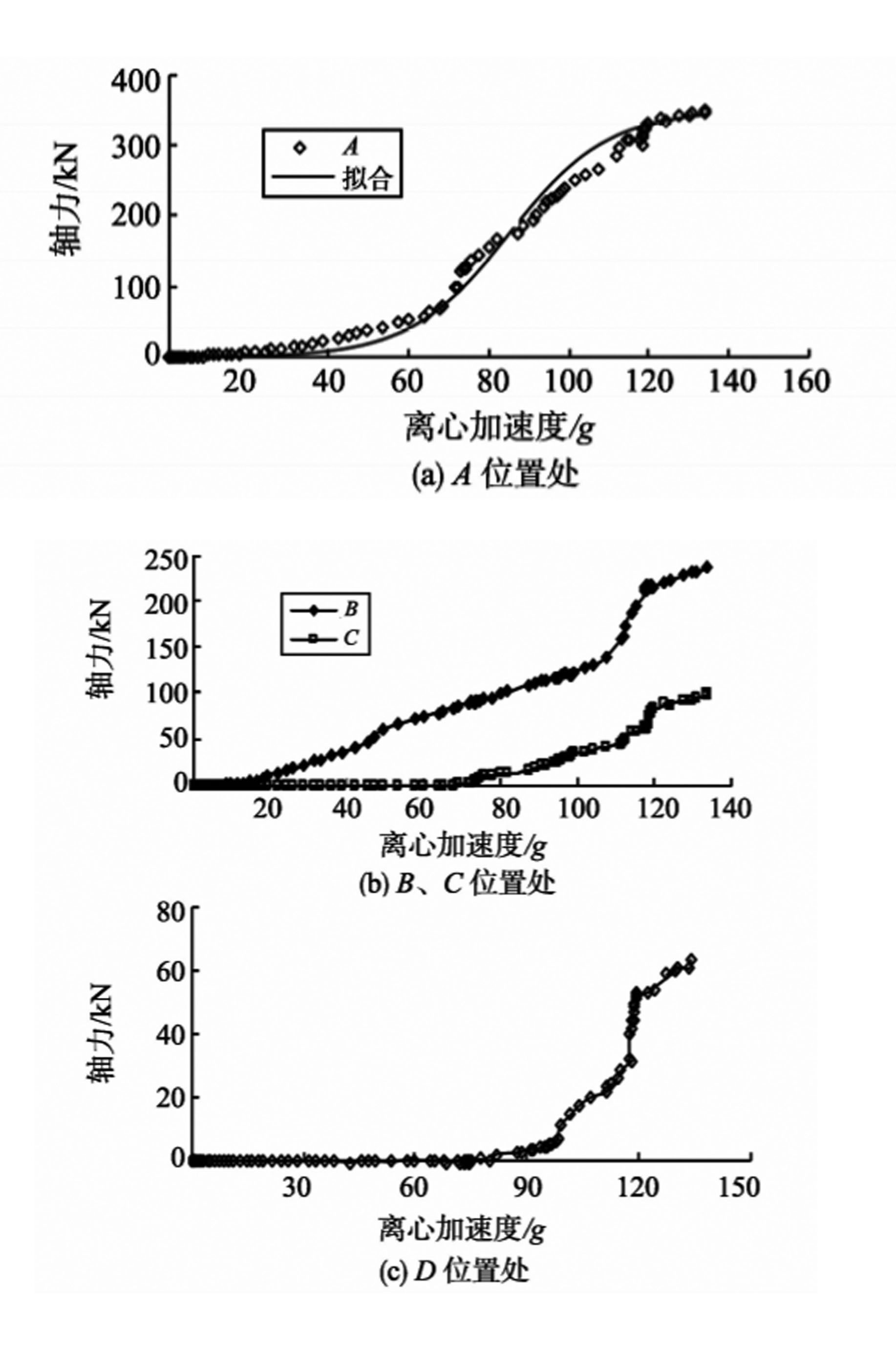
图9为锚杆轴力随离心加速度的变化曲线。应力监测的结果显示,A处锚杆轴力最大,图9中可以得出边坡破坏时的离心加速度为135.1g,最大轴力为349.7 kN。该结构面控制岩质边坡的应力监测部位应以上部结构面为主。根据曲线形态,采用Logistic曲线对应力监测曲线进行拟合。对曲线A进行拟合的结果如式(4),相关系数为0.93,拟合度较高,拟合曲线与原曲线的对比如图9(a)所示,拟合曲线符合监测曲线的走势。
$$y = {{349.7} \over {1 + {{\rm{e}}^{ - 0.081\left( {x - 85.02} \right)}}}}$$
(4)
|
图9 结构面控制岩质边坡锚杆轴力-加速度曲线 Fig.9 Curves of rock bolt axial force and acceleration of structure plane controlled rock slope |
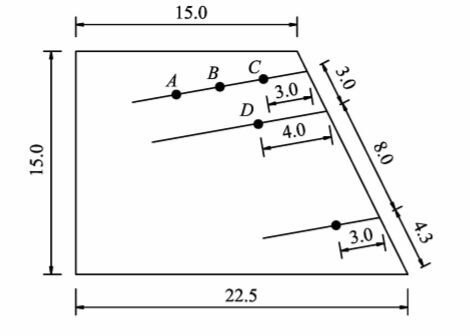
碎裂结构岩质边坡采用碎石加泥浆材料胶结的方式作为岩体替代材料,参照文献[13]所采用替代材料选择如下:碎石材料粒径5~10 mm,加泥浆胶结[13],泥浆强度参数为粘聚力c=13 kPa,内摩擦角φ=25°。试验设计方案如图10所示,边坡高度为15 cm,边坡坡度为1.0:0.5,选择锚杆与水平面夹角为10°。
|
图10 碎裂结构岩质边坡模型 Fig.10 Loosen structure rock slope model |
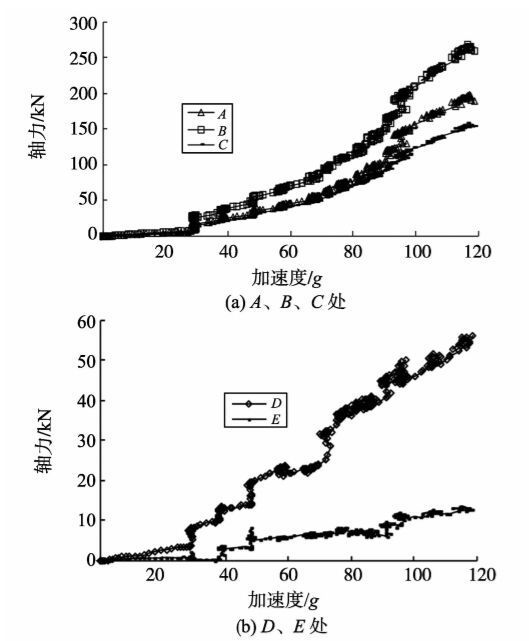
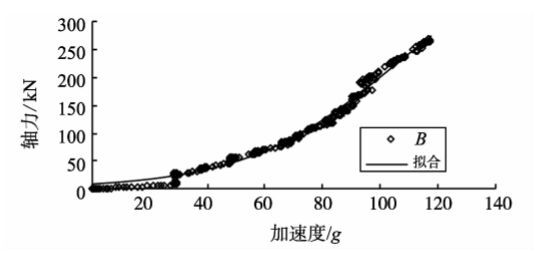
碎裂结构岩质边坡的破坏形式如图11所示,边坡破坏以上部破坏为主。与文献[13]试验结果相类似,表明了该试验结果的准确性[13]。图12为锚杆轴力随离心加速度的变化曲线。应力监测的结果显示,边坡在116.5g时发生破坏,最大轴力为位置B处的262.1 kN。根据曲线形态,采用 Logistic 曲线对应力监测曲线进行拟合。对曲线B进行拟合的结果如式(5),公式相关系数为0.94,拟合度高,拟合曲线与原曲线的对比如图13所示,符合曲线的走势。
$$y = {{447.76} \over {1 + {{\rm{e}}^{ - 0.038\left( {x - 105.38} \right)}}}}$$
(5)

|
图11 碎裂结构岩质边坡失稳图 Fig.11 Failure figure of loosen structure rock slope |
|
图12 碎裂结构岩质边坡锚杆轴力-加速度曲线 Fig.12 Curves of rock bolt axial force and acceleration of loosen structure rock slope |
|
图13 碎裂结构岩质边坡锚杆轴力-加速度拟合曲线 Fig.13 Fit curve of rock bolt axial force and acceleration of loosen structure rock slope |
利用离心模型试验对典型岩质边坡的应力监测过程进行模拟,在验证应力监测适用于岩质边坡稳定性评价的基础上,得出如下结论:
(1) 顺层滑动岩质边坡的应力监测结果表明,应力监测变化曲线平稳,无突变存在,监控过程易于把握,监测部位应以滑动面下部为主;
(2) 试验所选取的结构面控制破坏的岩质边坡类型,应力监测部位应以上部结构面为主,其他破坏形式的边坡监测位置需进一步研究确定;
3) 碎裂结构岩质边坡的监测部位应以边坡上部为主;
(4) 三类不同岩质边坡失稳过程中的锚杆轴力变化规律均符合 Logistic 型曲线形式,且拟合的相关系数较高,表明在离心试验条件下,不同类型岩质边坡失稳前的内部应力变化规律具有相通性。
| [1] | 曹洁,张嘎,王丽萍. 土钉加固黏性土坡加载的离心模型试验研究[J]. 岩土力学, 2012, 33(6):1696-1702. CAO Jie, ZHANG Ga,WANG Liping. Centrifugal model test on behavior of strip footing on soil nail-reinforced cohesive soil slopes[J]. Rock and Soil Mechanics, 2012, 33(6):1696-1702.(  1) 1) |
| [2] | 李明,张嘎,胡耘, 等. 边坡开挖破坏过程的离心模型试验研究[J]. 岩土力学, 2010, 31(2):366-370. LI Ming, ZHANG Ga, HU Yun, et al. Centrifugal model test on behavior of strip footing on soil nail-reinforced cohesive soil slopes[J]. Rock and Soil Mechanics, 2010, 31(2):366-370.(  1) 1) |
| [3] | TOHARI A, NISHIGAKI M, KOMATSU M.Laboratory rainfall-induced slope failure with moisture content measurement[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2007, 133(5):575-587.( 1) 1) |
| [4] | 周浩,郭永建,郭风明,等. 利用离心模型试验求解岩质边坡抗滑稳定安全系数[J]. 南水北调与水利科技, 2012,10(1):27-30. ZHOU Hao, GUO Yongjian, GUO Fengming, et al. Using geotechnical centrifuge model test to solve rock slope safety factor against sliding[J]. South-to-North Water Diversion and Water Science & Technology, 2012, 10(1):27-30.(  1) 1) |
| [5] | BRAY J W, GOODMAN R E. The theory of base friction models[J]. International Journal of Rock Mechanics and Mining Science & Geomechanics Abstracts, 1981, 18:453-468.( 1) 1) |
| [6] | GOODMAN R E. Introduction to rock mechanics[M]. New York:John Willey and Sons Incorporated, 1989.( 1) 1) |
| [7] | GOODMAN R E. Block theory and its application[J]. Geotechnique, 1995, 45(3):383-422.( 1) 1) |
| [8] | STEWART D P, ADHIKARY D P, JEWELL R J. Studies on the stability of model rock slopes[C]//Proceedings of the InternationalConference on Centrifuge 94. Singapore: A A Balkema, 1994: 629-634.( 1) 1) |
| [9] | CHEN Z Y, ZHANG J H, WANG W X. Centrifuge modeling for rock slopes[C]//Physical Modelling in Geotechnics-6th ICPMG′06. Hong Kong, China: Taylor & Francis Group, 2006:19-28.( 1) 1) |
| [10] | ZHANG J H, CHEN Z Y. Centrifuge modeling of rock slopes susceptible to block toppling[J]. Rock Mechanics and Rock Engineering, 2007, 40(4):363-382.( 1) 1) |
| [11] | 汪小刚,张建红,赵毓芝, 等. 用离心模型研究岩石边坡的倾倒破坏[J]. 岩土工程学报,1996,18(5):14-21. WANG Xiaogang, ZHANG Jianhong, ZHAO Yuzhi, et al. Investigations on mechanism of slope toppling failure by centrifuge model testing[J]. Chinese Journal of Geo-technical Engineering, 1996, 18(5):14-21.(  1) 1) |
| [12] | 陈祖煜, 汪小刚, 杨健, 等.岩石边坡稳定分析—原理·方法·程序[M]. 北京:中国水利水电出版社, 2005.( 1) 1) |
| [13] | 邓卫东, 吴光勇, 唐树名. 路堑边坡破坏机理的试验与计算分析[J].中国公路学报,2001,14(3):21-23. DENG Weidong, WU Guangyong, TANG Shuming. Test and calculation on the failure of cutting slope[J]. China Journal of Highway and Transport, 2001, 14(3):21-23.(  3) 3) |
| [14] | 唐红梅,陈洪凯,曹卫文. 顺层岩体边坡开挖过程模型试验[J]. 岩土力学, 2011, 32(2):435-440. TANG Hongmei, CHEN Hongkai, CAO Weiwen. Model experiment in excavation of rock bedding[J]. Rock and Soil Mechanics, 2011, 32(2):435-440.(  1) 1) |
| [15] | 冯振,殷跃平,李滨, 等. 斜倾厚层岩质滑坡视向滑动的土工离心模型试验[J].岩石力学与工程学报, 2012, 31(5):890-897. FENG Zhen, YIN Yueping, LI Bin, et al. Centrifuge modeling of apparent dip slide from oblique thick bedding rock landslide[J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(5):890-897.(  1) 1) |
| [16] | 张强勇, 李术才, 郭小红, 等. 铁晶砂胶结新型岩土相似材料的研制及其应用[J]. 岩土力学, 2008, 29(8):2126-2130. ZHANG Qiangyong, LI Shucai, GUO Xiaohong, et al. Research and development of new typed cementitious geotechnical similar material for iron crystal sand and its application[J]. Rock and Soil Mechanics, 2008, 29(8):2126-2130.(  1) 1) |
| [17] | 张宁,李术才,李明田,等. 新型岩石相似材料的研制[J]. 山东大学学报(工学版), 2009, 39(4):149-154. ZHANG Ning, LI Shucai, LI Mingtian, et al. Development of a new rock similar material[J]. Journal of Shandong University(Engineering Science), 2009, 39(4):149-154.(  1) 1) |
| [18] | 王汉鹏, 李术才, 张强勇, 等. 新型地质力学模型试验相似材料的研制[J]. 岩石力学与工程学报, 2006, 25(9):1842-1847. WANG Hanpeng, LI Shucai, ZHANG Qiangyong, et al. Development of a new geomechanical similar material[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(9):1842-1847.(  1) 1) |
| [19] | 栗东平, 王谦源, 张增祥, 等. 模拟岩性的相似试验研究[J]. 河北工程大学学报(自然科学版), 2007, 24(2): 12-14. LI Dongping, WANG Qianyuan, ZHANG Zengxiang, et al. Similar test research on property of simulated rock[J]. Journal of Hebei University of Engineering(Natural Science Edition), 2007, 24(2):12-14.(  1) 1) |
| [20] | 郭永建, 谢永利, 牛富生. 公路岩质边坡应力监测离心模型试验与应用[J]. 同济大学学报(自然科学版), 2013, 41(11): 1897-1701. GUO Yongjian, XIE Yongli, NIU Fusheng. Centrifugal model test research and application on stress monitoring for highway rock slope[J]. Journal of Tongji University(Natural Science), 2013, 41(11):1697-1701.(  1) 1) |
| [21] | 方开泰,许建伦. 统计分析[M].北京:科学出版社,1987.( 1) 1) |
| [22] | 李宗坤, 郑晶星, 王伟. 基于双曲线回归三参模型的分析方法研究[J]. 郑州大学学报(工学版), 2002, 23(1):14-17. LI Zongkun, ZHENG Jingxing, WANG Wei. Study on method of analysis based on hyperbola regression three-parameter model[J]. Journal of Zhengzhou University(Engineering Science), 2002, 23(1):14-17.(  1) 1) |
| [23] | 王济川,郭志刚. Logistic回归模型—方法与应用[M].北京:高等教育出版社,2001.( 2) 2) |
| [24] | 张宏博,李英勇,宋修广. 边坡锚固工程中锚索预应力的变化研究[J]. 山东大学学报(工学版), 2002, 32(6):574-577. ZHANG Hongbo, LI Yingyong, SONG Xiuguang. On prestress variation of cable in reinforcement engineering of slope[J]. Journal of Shandong University(Engineering Science), 2002, 32(6):574-577.(  1) 1) |
| [25] | 彭作为, 周创兵, 龚玉峰,等.向家坝进水口高边坡系统锚杆受力状况研究[J].岩土力学, 2006, 27(3):482-486. PENG Zuowei, ZHOU Chuangbing, GONG Yufeng, et al. Mechanical analysis of systematic bolts on rock mass in high side slope at intake of Xiangjiaba Hydropower Station[J]. Rock and Soil Mechanics, 2006, 27(3):482-486.(  1) 1) |



