2.中国气象局气象干部培训学院河北分院, 河北 保定 071000;
3. 河北大学计算机科学与技术学院, 河北 保定 071002)
2. Hebei Branch of Meteorological Cadres Training Institute, China Meteorological Administration, Baoding 071000, Hebei, China;
3. School of Computer Science and Technology, Hebei University, Baoding 071002, Hebei, China
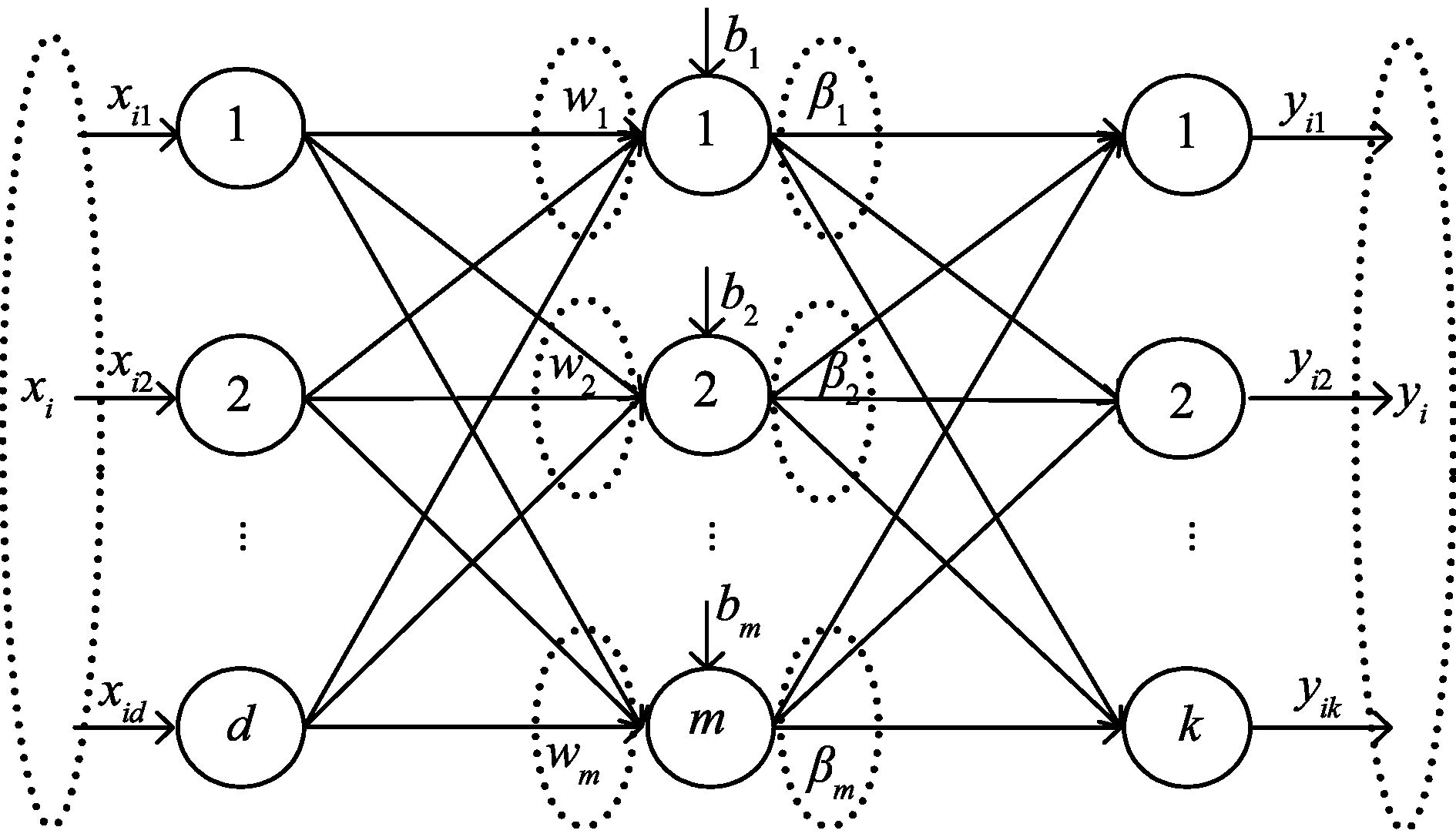
极限学习机(extreme learning machine,ELM)[1, 2, 3]是黄广斌等人提出的一种训练单隐含层前馈神经网络(single-hidden layer feed-forward neural networks,SLFNNs) (见图1)的简单而有效的算法。ELM随机生成输入层的权值和隐含层结点的偏置,用分析的方法确定输出层的权值,黄广斌等人证明了ELM具有一致逼近能力[4]。 实际上,在ELM算法中,输入层到隐含层所起的作用是一个随机映射,它把训练集中的样本点由原空间映射到了一个特征空间。 特征空间的维数由隐含层结点的个数确定。 一般地,这个特征空间的维数比原空间的维数高。 与其它的SLFNNs训练算法(如反向传播算法[5, 6, 7]、支持向量机算法[8, 9, 10, 11])相比,ELM 的优点是不需要迭代调整权参数,具有非常快的学习速度和非常好的泛化能力。
近几年,ELM已成为机器学习领域的研究热点之一。 不同研究人员提出了不同的ELM扩展算法,如针对增量学习问题的I-ELM(Incremental ELM)[12]、针对在线序列学习问题的OS-ELM (Online Sequential ELM)[13]、针对网络结构学习问题的OP-ELM(Optimally Pruned ELM)[14]等。 这些算法都是针对图1所示的单隐含层前馈神经网络的训练算法。
|
图1 单隐含层前馈神经网络 Fig.1 Single-hidden layer feed-forward neural network |
2004年,黄广斌等人将ELM算法推广到了径向基函数神经网络(radial basis function neural networks,RBFNNs) (见图2)的情况 [15],提出了RBF-ELM算法。该算法是训练RBF网络的算法,它的基本思想和ELM算法一样,它随机生成径向基函数的中心参数和宽度参数,用分析的方法确定RBF网络的权值。RBF-ELM具有ELM的所有优点,如学习速度快、泛化能力强等。但RBF-ELM和ELM都具有如下的一些缺点[16]:
(1) 由随机映射产生的预测不稳定性问题;
(2) 高维数据学习的过拟合问题;
(3) 隐含层输出矩阵的高维计算问题;
(4) 网络结构难于确定问题。
针对上述问题,本研究提出了核心集径向基函数极限学习机 (Core-Set based RBF-ELM,CS-RBF-ELM),它只随机初始化宽度参数,中心参数用核心集初始化。该算法不仅可以在一定程度上解决RBF-ELM的不稳定性问题,还可以提高算法的测试精度。此外,提出的算法还可以确定隐含层结点的个数。试验结果表明该算法优于RBF-ELM。

|
图2 径向基函数网络 Fig.2 Radial basis function neural network |
图2中,i(·),i=1,2,…,m是核函数,一般情况下它是如公式(1)所示的高斯核函数。
| \[{\phi _i}\left( x \right) = \phi \left( {x,{\mu _i},{\sigma _i}} \right) = \exp \left( {\frac{{{{\left\| {x - {\mu _i}} \right\|}^2}}}{{{\sigma _i}}}} \right)\] | (1) |
其中,μi=(μi1,…,μid)T是第i个核函数的中心,σi是宽度参数。 βi=(βi1,…,βim)T是连接第i个核函数和输出神经元的权向量。对于给定的输入x∈Rd,具有m个核函数的RBFNN的输出
| \[f\left( x \right) = |\sum\limits_{i = 1}^m {{\beta _i}} {\phi _i}\left( x \right)\] | (2) |
给定一个训练集D={(xi,ti)},xi∈Rd,ti∈Rk,i=1,2,…,n。 如图2所示的RBFNN可表示为
| \[\sum\limits_{j = 1}^n {{\beta _j}} ,j = 1,2, \cdots ,n\] | (3) |
具有m个核函数的RBFNN以0误差逼近n个不同的样例,即
| \[\sum\limits_{j = 1}^n {\left\| {{o_j} - {t_j}} \right\|} = 0\] | (4) |
换句话说,存在βi,μi和σi,使得下面的公式(5)成立:
| \[\sum\limits_{j = 1}^n {{\beta _i}} \exp \left( {\frac{{{{\left\| {x - {\mu _i}} \right\|}^2}}}{{{\sigma _i}}}} \right) = {t_j},j = 1,2, \cdots ,n\] | (5) |
公式(5)可以写成如下的矩阵形式:
| \[H\beta = T\] | (6) |
| \[H=\left[ \begin{matrix} \phi \left( {{x}_{1}},{{\mu }_{1}},{{\sigma }_{1}} \right) & \cdots & \left( {{x}_{1}},{{\mu }_{m}},{{\sigma }_{m}} \right) \\ \vdots & \ddots & \vdots \\ \phi \left( {{x}_{n}},{{\mu }_{n}},{{\sigma }_{n}} \right) & \cdots & \phi \left( {{x}_{n}},{{\mu }_{m}},{{\sigma }_{m}} \right) \\ \end{matrix} \right]\] |
| \[\begin{gathered} \beta = {\left( {\beta _1^{\text{T}}, \cdots ,\beta _m^{\text{T}}} \right)^T} \hfill \\ T = {\left( {t_1^{\text{T}}, \cdots ,t_n^{\text{T}}} \right)^T} \hfill \\ \end{gathered} \] |
与ELM中一样,公式(6)的最小二乘解可通过求解下面的优化问题得到。
| \[\mathop {\min }\limits_\beta \left\| {H\beta | - T} \right\|\] | (7) |
通过求矩阵H的伪逆矩阵,优化问题(7)的最小范式二乘解可由下式求得,
| β=H†T |
其中,H†T是H的伪逆矩阵。
RBF-ELM算法可描述如下。
算法 1 RBF-ELM
输入: 训练集D={(xi,ti)},i=1,…,n,核函数,核函数的个数m
输出: 权矩阵β
第一步: 随机初始化核函数的中心参数μi和宽度参数σi,i=1,…,m;
第二步: 计算隐含层输出矩阵H;
第三步: 计算权矩阵 β=H†T。
2 核心集径向基函数极限学习机本节介绍提出的核心集径向基函数极限学习机算法。该算法分为两个阶段,第一个阶段利用核心集算法计算核心集,并用核心集作为RBFNN的中心;第二个阶段随机初始化核函数的宽度参数,并用RBF-ELM训练径向基函数网络,求得输出层权矩阵。下面首先介绍核心集及计算核心集的算法,然后给出基于核心集的径向基函数极限学习机算法。
2.1 核心集从求解最优化问题的角度,一个点集的核心集是它的一个子集,使得在核心集上求解优化问题得到的解,可以很好地逼近原问题的解[17, 18]。下面以最小包围球问题为例,介绍寻找核心集的算法。对于给定的一个点集S,最小包围球问题是计算能包围点集S的球的最小半径。
设Bc,r表示球心在c∈Rd、半径为r的球。给定Rd中的一个点集S={x1,x2,…,xn},每一个点是一个样例。S的最小包围球MES(S)是包含S的半径最小的球。
定义 1 设c*是MES(S)的球心,r*是MES(S)的半径。给定ε>0,如果r≤r*,而且SBc,(1+ε)r,则称球Bc,(1+ε)r为MES(S)的(1+ε)-近似(或扩展) [18]。
定义 2 给定ε>0,XS,如果Bc,(1+ε)rS,Bc,r=MEB(X),则称X为S的核心集[18]。
定义2可解释为:如果MES(X)的(1+ε)-近似(或扩展)包含集合S,则X为S的核心集。
关于核心集,有下面两个重要的性质[17]。
性质 1 Rd中任何一个点集,都有一个大小为 $\left\lceil {\frac{1}{\varepsilon }} \right\rceil $的核心集,而且这个界是最坏情况下的紧下届。
性质 2 一个集合的核心集的大小和维数d没有关系。
这两个性质非常有用,对于控制核心集的大小及核心集在高维空间中的应用具有指导意义,如TSANG I W等将核心集应用于SVM,提出了著名的核向量机算法[19]。下面给出寻找核心集的算法[18]。
算法 2 计算核心集的算法
输入: S={x1,x2,…,xn}∈Rd,ε>0
输出: 核心集X
第一步: 初始化X;
第二步: 计算Bc,r=MEB(X);
第三步: 如果SBc,(1+ε)r,则输出X;否则进入第四步;
第四步: 在S中找距离c最远的点p;
第五步: X=X∪{p},然后转第二步。
算法第一步是从集合S中任选一个点p,然后找距离p最远的点q,再找距离q最远的点t,用集合{q,t}初始化X。
2.2 核心集径向基函数极限学习机给定一个训练集D={(xi,ti)},xi∈Rd,ti∈Rk,i=1,2,…,n。两阶段的核心集径向基函数极限学习机可描述如下。
算法 3 核心集径向基函数极限学习机(CS-RBF-ELM)
输入: 训练集D={(xi,ti)},i=1,…,n,半径扩展参数ε>0,核函数的个数m
输出: 权矩阵β
第一个阶段: 确定RBF的中心
利用算法2计算训练集D的核心集X,并用核心集X初始化RBF的中心,假设|X|=m。
第二个阶段: 利用ELM训练RBFNN
(1) 随机生成宽度参数σi(1≤i≤m);
(2) 计算隐含层的输出矩阵H;
(3) 计算输出权重矩阵β=H†T。
3 试验结果为验证CS-RBF-ELM算法的有效性,采用对比试验的方法,在10个UCI数据集[20](见表1)上与传统RBF-ELM算法进行对比。对比的性能指标包括测试精度、隐含层结点数和计算时间。此外,还进一步用试验的方法研究半径扩展参数ε对测试精度的影响及半径扩展参数与计算时间之间的关系。
| 表1 试验所用数据集的基本信息 Table 1 Basic information of the data sets used in the experiments |
试验结果见表2。可以看出,CS-RBF-ELM两阶段学习算法与传统的RBF-ELM算法相比,除Page Block数据集外,在其它数据集上CS-RBF-ELM算法的分类精度都高于RBF-ELM,所得到的网络结构更为紧凑。除Vehicle数据集外,在其它数据集上CS-RBF-ELM算法所用的时间均低于RBF-ELM。所以,总体上来说,提出的CS-RBF-ELM算法优于原始的RBF-ELM算法。
| 表2 与原始的RBF-ELM算法进行比较的试验结果 Table 2 The experimental results compared with original RBF-ELM |
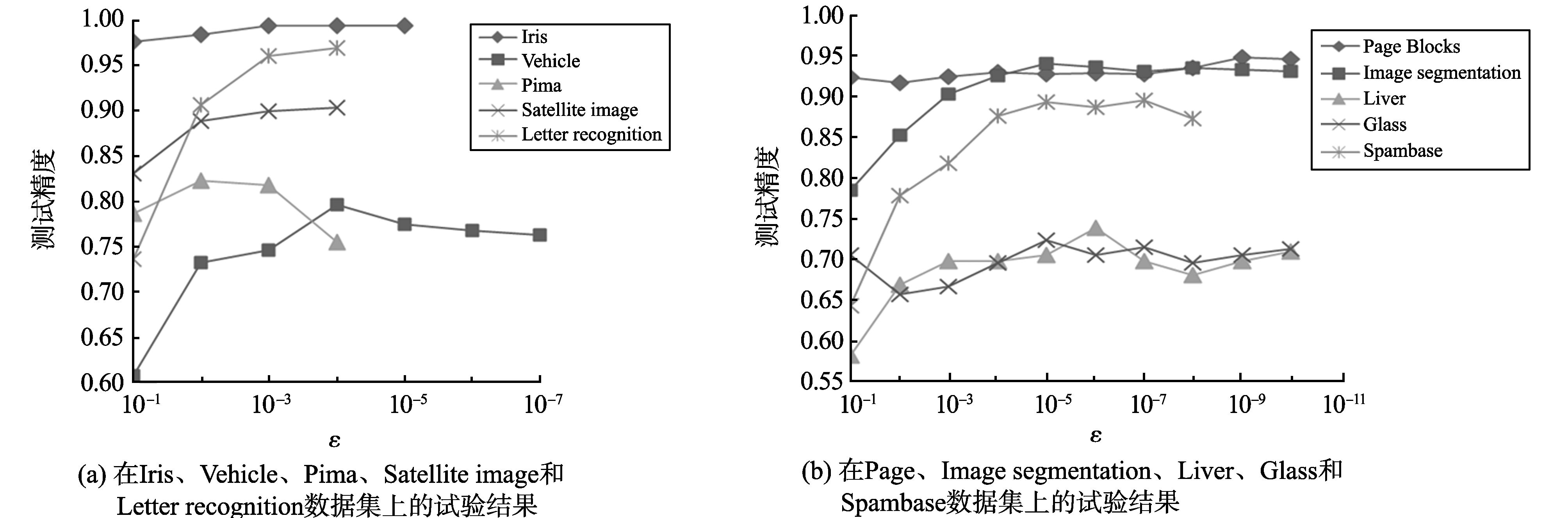
试验研究了半径扩展参数ε对测试精度的影响。在试验中,对于每一个数据集,让半径扩展参数ε逐渐变化,记录相应的测试精度,并绘制出变化曲线,如图3所示,其中在Iris、 Vehicle、 Pima、 Satellite image和Letter recognition数据集上的试验结果如图3(a)所示,在Page Block、Image segmentation、Liver、Glass和Spambase数据集上的试验结果如图3(b)所示。
|
图3 半径扩展参数ε与测试精度之间的关系 Fig.3 Relationship between the extension parameter of ε and testing accuracy |
关于半径扩展参数ε与计算时间t之间的关系,做了类似的试验。在Iris、Page Block、Image segmentation、Liver和Glass数据集上的试验结果如图4(a)所示。在Vehicle、Pima、Satellite image、Letter recognition和Spambase数据集上的试验结果如图4(b)所示。

|
图4 半径扩展参数ε与计算时间之间的关系 Fig.4 Relationship between the extension parameter of radius ε and computing time |
从图3可以看到,随着ε的减小,测试精度不断升高,当ε减小到一定程度时,二者将不再增加而是趋于稳定,提出的算法CS-RBF-ELM可以在一定程度上解决RBF-ELM算法的预测不稳定性问题。显然,随着ε值减小,分类精度得到提高,但要花费更多的计算时间。
从图4可以看到,计算时间随ε的减小成指数倍增加。并且在同一ε值下,在较小数据集上的计算时间相对较大数据集短,如Iris数据集与Image Segmentation数据集相比;数据集的类别数越多计算时间越长,如Glass与Liver Disorders相比;数据集条件属性数越多计算时间也越长,如Letter Recognition与Page Blocks相比。以上的结论显然也是符合客观规律的。
4 结语针对原始RBF-ELM存在的预测不稳定及结构难于确定问题,提出了一种改进RBF-ELM算法,它只随机初始化宽度参数,中心参数用核心集初始化。提出的算法不仅可以在一定程度上解决RBF-ELM的不稳定性问题,还可以提高算法的测试精度。同时,提出的算法还可以确定RBF-ELM网络的结构,试验结果证明提出的算法优于RBF-ELM算法。
| [1] | HUANG Guangbin, ZHU Qinyu, SIEW C K. Extreme learning machine: A new learning scheme of feedforward neural networks[C]//Proceedings of International Joint Conference on Neural Networks (IJCNN2004). Budapest, Hungary: IJCNN, 2004:985-990.( 1) 1) |
| [2] | HUANG Guangbin, ZHU Qinyu, SIEW C K. Extreme learning machine: Theory and applications[J]. Neurocomputing, 2006, 70(1-3):489-501.( 1) 1) |
| [3] | HUANG Guangbin, WANG Dianhui, LAN Yuan. Extreme learning machines: a survey[J]. International Journal of Machine Learning and Cybernetics, 2011, 2(2):107-122.( 1) 1) |
| [4] | HUANG Guangbin, CHEN Lei, SIEW C K. Universal approximation using incremental constructive feedforward networks with random hidden nodes[J]. IEEE Transactions on Neural Networks, 2006, 17(4):879-892.( 1) 1) |
| [5] | KUMAR S. Neural network[M]. Beijing: Tsinghua University Press, 2006.( 1) 1) |
| [6] | 高小伟, 蒋晓芸. BP神经网络在入侵检测系统中的应用及优化 [J]. 山东大学学报(工学版), 2006, 36(6):107-110. GAO Xiaowei, JIANG Xiaoyun. The application of BP neural network in intrusion detection system and its optimization[J]. Journal of Shandong University(Engineering Science), 2006, 36(6):107-110.. ( 1) 1) |
| [7] | 姚福安, 庞向坤, 焦营营,等. 基于三色法和BP神经网络的回转窑温度检测[J]. 山东大学学报(工学版), 2008,38(2):61-65. YAO Fuan, PANG Xiangkun, JIAO Yingying, et al. Temperature detection of a rotary kiln based on three color measurement and the BP neural network[J]. Journal of Shandong University(Engineering Science), 2008, 38(2):61-65.( 1) 1) |
| [8] | VAPNIK V. The nature of statistical learning theory[M]. New York: Springer, 1995.( 1) 1) |
| [9] | 赵加敏,冯爱民,刘学军. 局部密度嵌入的结构单类支持向量机[J]. 山东大学学报(工学版), 2012,42(4):14-18. ZHAO Jiamin, FENG Aimin, LIU Xuejun. A new structured one-class support vector machine with local density embedding[J]. Journal of Shandong University(Engineering Science), 2012, 42(4):14-18.( 1) 1) |
| [10] | 施珺, 朱敏. 一种基于灰色系统和支持向量机的预测优化模型[J]. 山东大学学报(工学版), 2012, 42(5):7-11. SHI Jun, ZHU Min. An optimization model for forecasting based on grey system and support vector machine [J]. Journal of Shandong University(Engineering Science), 2012, 42(5):7-11.( 1) 1) |
| [11] | 王雪松, 程玉虎, 郝名林. 一种支持向量机参数选择的改进分布估计算法[J]. 山东大学学报(工学版), 2009,39(3):7-10. WANG Xuesong, CHENG Yuhu, HAO Minglin. Parameters selection of a support vector machine using an improved estimation of the distribution algorithm[J]. Journal of Shandong University(Engineering Science), 2009, 39(3):7-10.( 1) 1) |
| [12] | HUANG Guangbin, LI Mingbin, CHEN Lei, et al. Incremental extreme learning machine with fully complex hidden nodes[J]. Neurocomputing, 2008, 71(4-6):576-583.( 1) 1) |
| [13] | LIANG Nanning, HUANG Guangbin, SARATCHANDRAN P, et al. A fast and accurate online sequential learning algorithm for feedforward networks[J]. IEEE Transactions on Neural Networks, 2006, 17(6):1411-1423.( 1) 1) |
| [14] | MICHE Y, SORJAMA A, BAS P, et al. OP-ELM: Optimally pruned extreme learning machine[J]. IEEE Transactions on Neural Networks, 2010, 21(1):158-162.( 1) 1) |
| [15] | HUANG Guangbin, SIEW C K. Extreme Learning Machine: RBF Network Case[C]//Proceedings of Conference on Control, Automation, Robotics and Vision. Kunming, China: CARV, 2004:1029-1036.( 1) 1) |
| [16] | ZHAI Junhai, XU Hongyu, WANG Xizhao. Dynamic ensemble extreme learning machine based on sample entropy[J]. Soft Computing September, 2012, 16(9):1493-1502.( 1) 1) |
| [17] | BADOIU M, CLARKSON K L. Optimal core-sets for balls[J]. Computational Geometry, 2008, 40(1):14-22.( 2) 2) |
| [18] | KUMAR P, MITCHELL J, YILDIRIM A. Approximate minimum enclosing balls in high dimensions using core-sets[J]. ACM Journal of Experimental Algorithmics, 2003(8):1-29.( 3) 3) |
| [19] | TSANG I W, KWOK J T, CHEUNG P M. Core vector machines: Fast SVM training on very large data sets[J]. Journal of Machine Learning Research, 2005(6):363-392.( 1) 1) |
| [20] | FRANK A, ASUNCION A. UCI Machine Learning Repository[EB/OL][2013-10-05].( 1) 1) |



