灵沼轩俗称水晶宫,位于故宫东六宫的延禧宫内。该建筑始建于1909年,主要用于皇家休闲时观鱼赏景,后因国库空虚而被迫停建^{[1, 2, 3]}。建筑形式属西洋式风格,建筑地下1层,地上2层,平面尺寸为24.73 m×18.57 m,总高度14.62 m。结构形式为工字钢梁及铸铁柱为核心承重框架,前后檐及四周围廊为汉白玉砌体结构。另中间钢框架顶部设双层八角形铁亭,四周围廊顶部设多边形单层铁亭,合计铁亭5座。

灵沼轩钢结构属我国现存为数不多的钢结构文物建筑,含有丰富的历史和文化信息,保护意义重大。然而由于历经年代长久,在不同因素作用下,该结构出现了较为明显的残损问题。经勘查,结构主要残损症状包括非主要承重铁件锈蚀及缺失、部分梁柱结点(为避免冲突,本研究称梁柱交点为结点、有限元模型点单元为节点)锈蚀、部分位置的铸铁柱存在开裂。文献[4, 5]报道,灵沼轩钢铁质构件的主要锈蚀机理为大气环境下的电化学腐蚀,其所处的外部环境及自身的材质、加工特点,均可对锈蚀程度产生影响;而金属构件的断裂、变形,除了构件自身的材料特性外,还与其承受的构造应力、环境高低温交变以及不恰当的填充材料有关。

从恢复灵沼轩建筑整体原貌角度考虑,本研究的重点是灵沼轩工字钢梁-铸铁柱承重框架的抗震性能。关于钢结构整体及半刚性结点的抗震性能研究,国内外已有不少报道,如陈宏等通过数值模拟和试验方法,研究了两类螺栓端板连接钢结点的承载性能和刚度特征,获得了钢结点的弯矩-转角曲线^[6];黄冀卓等通过半解析测试方法获取钢结构梁柱连接结点的半刚性特性,并提出了一种有效的求解结点刚度的半解析测试方法^{[7, 8]};杜俊等以一阶横向振动周期、结构梁柱轴力比和层间位移限角为评价指标,研究了梁柱半刚性连接对钢结构整体抗震性能的影响,认为结点横向弯曲刚度对结构抗震性能影响显著^{[9, 10]}; ATOROD A和JAMES B R采用试验方法,获得了腹板带双角钢的上下翼缘角钢连接结点的结点转角刚度范围^[11];HONG K等采用静力加载试验方法,研究了钢结点初始刚度和最终承载力的影响因素^[12]。然而基于钢结构结构残损现状及结点刚度退化的抗震性能相关研究,以及对灵沼轩钢结构本身抗震性能的研究,现有成果较少。基于此,本研究采取有限元分析方法,研究灵沼轩钢结构的动力特性及地震响应情况,讨论钢结点刚度退化对结构整体抗震性能的影响,结果可为钢结构文物的保护和维修提供理论参考。

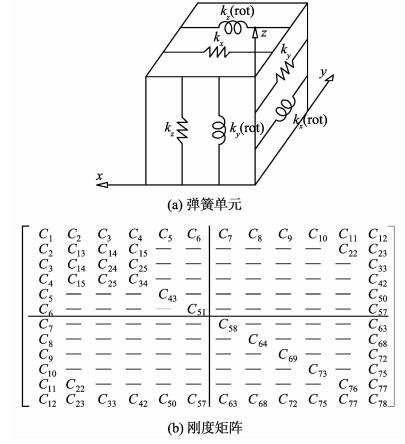
本研究采用有限元分析程序ANSYS分析灵沼轩钢结构动力特性及抗震性能。灵沼轩钢结构框架的梁和柱采用螺栓连接,属于半刚性连接形式,可采用3维虚拟弹簧单元组来模拟^{[13, 14, 15]}。该弹簧单元组由6根互不偶联的弹簧组成,其刚度取值分别为k_x、k_y、k_z和k_x(rot)、k_y(rot)、k_z(rot),其中前3个参数分别表示沿x、y、z轴的拉压刚度,后3个参数表示绕x、y、z轴的转动刚度,见图 1(a)所示。

图 1(Fig. 1)

图 1 钢结点模拟方法 Fig. 1 Simulation method for steel joints

ANSYS有限元程序中的MATRIX27 单元可用于模拟上述虚拟弹簧^{[16, 17]}。MATRIX27单元没有定义几何形状,但是可通过两个结点反映单元的刚度矩阵特性,其刚度矩阵输出格式见图 1(b)所示。图 1(b)中,对应x方向弹簧刚度k_x矩阵元为C₁、C₇、C₅₈;对应y方向弹簧刚度k_y矩阵元为C₁₃、C₁₉、C₆₄;对应z方向弹簧刚度k_z矩阵元为C₂₄、C₃₀、C₆₉;对应绕x轴转动刚度k_x(rot)的矩阵元为C₃₄、C₄₀、C₇₃;对应绕y轴转动刚度k_y(rot)的矩阵元为C₄₃、C₄₉、C₇₆;对应绕z轴转动刚度k_z(rot)的矩阵元为C₅₁、C₅₇、C₇₈。在进行分析时,将上述弹簧刚度代入对应的矩阵元中即可获得半刚性结点刚度矩阵。

钢结点为半刚性连接,且历经时间变化后,在各种因素作用下会产生刚度退化现象。为研究钢结点刚度退化对其抗震性能影响,本研究从保守角度出发,考虑灵沼轩主体承重框架梁柱结点连接的3种工况,以表示钢结构在不同状态下的刚度特性,相关刚度参数取值见表 1^{[7, 8, 9, 10, 11, 12]}。其中,工况1近似表示钢结点连接处于较理想的状态;工况2近似表示钢结点历经长久时间后产生刚度退化时的状态(即现状),工况3则表示钢结点因时间长久,连接完全松动(铰接)时的状态。

表1(Table 1)

表1 梁柱结点刚度工况分类 Table 1 Classification of stiffness values of beam-column joints 工况 边界条件 kx=ky=kz/(N·m-1) kx(rot)=ky(rot)=kz(rot)/(N·m·rad-1) 1 半刚接 1.5×106 1.5×106 2 半刚接 1.5×106 1.5×103 3 铰接 1.5×106 0

表1 梁柱结点刚度工况分类 Table 1 Classification of stiffness values of beam-column joints

需要说明的是,本研究关注的重点为灵沼轩工字钢承重框架的抗震性能。其上部八角亭既属非承重构件,又尚未完工。因此,本研究讨论的上述钢结点刚度退化的不同工况条件仅针对工字钢承重框架而言,八角亭钢结点连接始终按工况1考虑。

2011年10月,国家建筑工程质量监督检验中心受故宫博物院委托,对灵沼轩钢结构进行了检测分析,认为灵沼轩钢结构柱为铸铁材料,其容许抗拉、压、弯强度f_c=544 MPa;工字钢梁材质为钢,容许抗拉、压、弯强度f_b=300 MPa^[18]。在进行有限元分析时,考虑梁柱材料均为线弹性,密度ρ=7 800 kg/m³,泊松比γ=0.3,弹性模量E=206 MPa。

基于研究目标,本研究考虑的力学分析模型为钢(铸铁)结构承重框架及顶部正中的铸铁八角亭。其他4个角亭由于嵌固在砌体围廊顶部,与承重工字钢框架无任何连接,因而暂不予考虑。主要承重框架的热轧工字钢梁截面尺寸为0.155 m×0.285 m×0.030 m×0.015 m(b×h×t×t_f)。铸铁柱柱径沿柱高产生变化,建模时,从保守角度考虑,取最小直径及壁厚处尺寸为柱计算截面尺寸,可得柱为圆环形截面,壁厚0.02 m,外径0.16 m。该处理方式使得结构安全性能评估的分析结果将偏于保守。

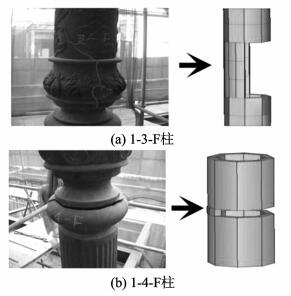
勘查发现,有2处铸铁柱存在明显开裂问题:1-3-F及1-4-F位置。1-3-F开裂柱裂纹底部离地面1.150 m,裂缝弯曲向上延伸,缝本身宽度为0.003 m,裂缝高度0.800 m,裂缝水平范围为1/2柱截面。建模时,仅考虑上述高度范围内的1/2宽度柱截面作为有效截面(图 2(a))。1-4-F柱裂缝位置在柱子中部最凹处,水平向,缝长占3/4圈,厚度约0.050 m,缝宽最大值达0.010 m。建模时,从保守角度出发,该位置有限元模型水平截面仅考虑1/4圈柱径为有效值(图 2(b))。

图 2(Fig. 2)

图 2 开裂柱及模拟方法 Fig. 2 Columns with cracks and corresponding simulation methods

钢结构承重框架的顶部正中为铸铁八角亭,立柱及连接板主要采用类似槽钢的异形铸铁材料制成,其有效截面尺寸为0.095 m×0.160 m×0.010 m×0.030 m(b×h×t×t_f),立柱顶部有工字钢用于支撑水箱,工字钢截面尺寸为0.125 m×0.300 m×0.030 m×0.015 m(b×h×t×t_f)。上述尺寸信息为灵沼轩有限元模型的构件截面尺寸确定依据。

灵沼轩钢结构由于历经时间长久,主要承重梁、柱构件均发生表面锈蚀,而螺栓则因锈蚀出现松动或掉落。在进行有限元建模时,相关梁柱的有效截面尺寸均为刨除梁柱表面锈蚀后的净尺寸。上述有效截面尺寸由故宫博物院古建部设计室参照国家建筑工程质量监督检验中心的分析报告提供。

经勘查,柱脚固定方式为将8根较长的竖向螺栓(d=30 mm)预埋在基底混凝土内,上部露明部分用螺栓将柱底盘中部(底盘边界距柱身的距离约150 mm)固定,柱础现状保持较好。由于在地震作用下,柱根产生转动的角度非常小,因而近似假设为固接方式。钢梁与墙体的连接方式包括2种:(1)大部分钢梁从楼板位置的墙身、墙外平台板直接穿过,由于该位置的墙体累计厚度约1.5 m,且现状基本完好,地震时钢梁产生转动的可能性很小,因而假定嵌固;(2) 钢梁做成斜梁形式,作为连接地面与灵沼轩建筑的栈桥。斜梁一端连接钢框架,另一端埋入水池侧壁,深度未知,但考虑为皇家建筑,其做法应该保守,因此亦考虑为固接。

本研究中,钢结构的边界条件包括2个方面:(1) 柱底及斜梁端部固接,共计18处约束点;(2) 由于墙体砌筑在框架内部,因而部分框架梁与墙体存在交点;上述位置的钢构件可认为受到墙体嵌固约束,按固接处理,计20处;以上共计38处约束点。

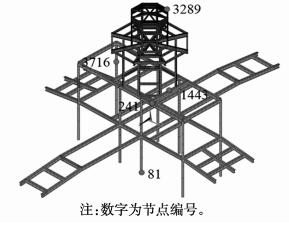
采用BEAM189单元模拟梁柱单元,基于上述构件的尺寸信息,并考虑梁柱结点的半刚性连接特性及边界约束条件,建立灵沼轩钢结构有限元模型,见图 3。

图 3(Fig. 3)

图 3 灵沼轩钢结构框架有限元模型 Fig. 3 Finite element model of steel structure of Ling-zhao Veranda

结构动力特性分析主要用于获得结构的自振频率、振型等动力性质参数,通过ANSYS有限元程序开展模态分析,可获得灵沼轩钢结构所需的动力特性参数^{[19, 20]}。

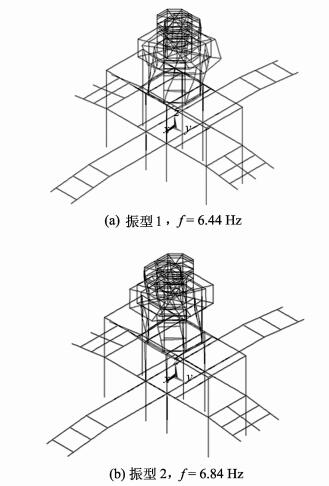
为研究灵沼轩钢结构的振动特性,对其进行模态分析,求得工况1条件下结构的前10阶频率及模态系数见表 2所示,相关主振型见图 4。

表2(Table 2)

表2 工况1振动分析结果 Table 2 Vibration analysis results of case 1 condition 阶数 频率/Hz 模态系数 x向 y向 1 6.44 0 1.00 2 6.84 1.00 0 3 12.14 0.60 0 4 15.23 0 0.10 5 28.67 0.14 0 6 43.17 0.17 0 7 46.40 0 0 8 47.61 0.10 0 9 49.02 0 0 10 49.10 0.10 0

表2 工况1振动分析结果 Table 2 Vibration analysis results of case 1 condition

图 4(Fig. 4)

图 4 工况1条件下灵沼轩钢结构主振型 Fig. 4 Main vibration modes of Ling-zhao Veranda under case 1 condition

本例中,x为水平纵向,y为水平横向,z为竖向。由表 2可知,工况1条件下,灵沼轩钢结构在纵向以第2振型为主,基频为6.44 Hz;在横向以第1振型为主,基频为6.84 Hz。另根据模态计算相关数据,灵沼轩钢结构在x、y、z向主振型的有效参与质量比例为1.37∶1.00∶0,即参与竖向振动的结构质量几乎为0,这说明灵沼轩钢结构振动以水平向为主。

由图 4可知,Mode 1振型中,结构沿y向产生侧向变形。上部八角亭侧向变形较明显;工字钢框架部分,除中部支撑八角亭的几根梁柱沿y向产生轻微侧向变形外,其余梁柱构件几乎未产生变形。其主要原因在于工字钢框架与墙体相交部分受到墙体嵌固作用,因而其振动变形受到约束。从变形引起的结构破坏角度考虑,上部八角亭部分,尤其是八角亭顶部因振动产生的变形明显大于其他部位,因而也是最容易产生破坏的位置。Mode 2 振型中,结构沿x向产生变形,变形特点及产生原因与Mode 1类似。

Mode 1与Mode 2的振动方向正交,说明两种振型的偶联性很小,即结构振动以平动为主,几乎不发生扭转,其主要原因是整个钢结构为对称布置。

该工况条件下灵沼轩钢结构的振动分析结果见表 3,主振型见图 5。分析知,灵沼轩钢结构在纵向以第10振型为主,基频为3.16 Hz;在横向以第8振型为主,基频同样为3.16 Hz。另根据模态计算相关数据,灵沼轩钢结构在x、y、z向主振型的有效参与质量比例为1∶1 ∶0,即参与竖向振动的结构质量几乎为0,这说明该工况条件下,灵沼轩钢结构振动以水平向为主。

表3(Table 3)

表3 工况2振动分析结果 Table 3 Vibration analysis results of case 2 condition 阶数 频率/Hz 模态系数 x向 y向 1 3.09 0.46 0.57 2 3.13 0.46 0.57 3 3.16 0 0.61 4 3.16 0.05 0.01 5 3.16 0 0.22 6 3.16 0 0.19 7 3.16 0 0.28 8 3.16 0 1.00 9 3.16 0.09 0 10 3.16 1.00 0

表3 工况2振动分析结果 Table 3 Vibration analysis results of case 2 condition

图 5(Fig. 5)

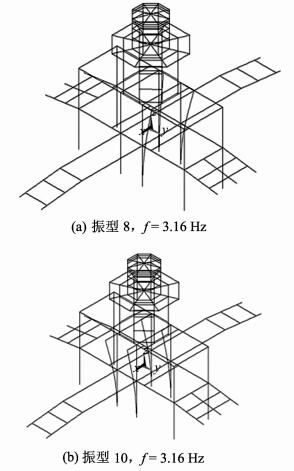
图 5 工况2条件下灵沼轩钢结构主振型 Fig. 5 Main vibration modes of Ling-zhao Veranda under case 2 condition

由图 5可知,Mode 8振型中,工字钢框架部分,除中部支撑八角亭的几根梁柱沿y向产生明显侧向变形外,其余梁柱构件几乎未产生变形。上部八角亭部分几乎未产生明显振动。这说明当承重钢框架刚度退化时,结构主要振动表现为中部承重框架的侧向变形。由于工字钢框架与墙体相交部分受到墙体嵌固作用,因而其振动变形仍受到约束。Mode 10振型特征与Mode 8相似,只不过前者表现为支撑八角亭的几根梁柱沿x向的侧向变形。

该工况条件下,结构主振型之间仍不存在偶联性,因而结构在地震作用下的振动仍以平动为主。

该工况条件下灵沼轩钢结构的振动分析结果见表 4,主振型见图 6。分析可知,灵沼轩钢结构在纵向以第5振型为主,基频为3.10 Hz;在横向以第3振型为主,基频为3.16 Hz。另根据模态计算相关数据,灵沼轩钢结构在x、y、z向主振型的有效参与质量比例为1 ∶1∶0,即参与竖向振动的结构质量几乎为0,这说明该工况条件下,灵沼轩钢结构振动仍以水平向为主。

表4(Table 4)

表4 工况3振动分析结果 Table 4 Vibration analysis results of case 3 condition 阶数 频率/Hz 模态系数 x向 y向 1 3.02 0.67 0.75 2 3.07 0.67 0.76 3 3.10 0.73 1.00 4 3.10 0.22 0.50 5 3.10 1.00 0.85 6 3.10 0.02 0.15 7 3.10 0.03 0.03 8 3.10 0.09 0.10 9 3.10 0.55 0.13 10 3.10 0.47 0.62

表4 工况3振动分析结果 Table 4 Vibration analysis results of case 3 condition

图 6(Fig. 6)

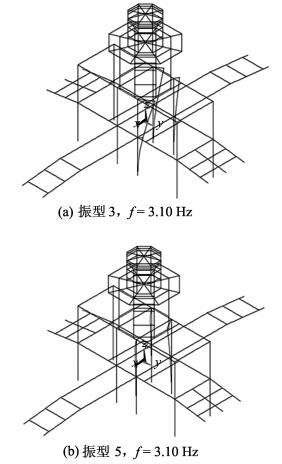
图 6 工况3条件下灵沼轩钢结构主振型 Fig. 6 Main vibration modes of Ling-zhao Veranda under case 3 condition

由图 6可知,Mode 3与Mode 5振型特征相似,即工字钢框架部分,除中部支撑八角亭的几根梁柱沿x-y对角方向产生明显侧向变形外,其余梁柱构件几乎未产生变形。上部八角亭部分仍未产生明显振动。这说明当钢结构结点完全松动时,结构振动形式发生明显变化。

由工况1～3的分析结果可以看出,灵沼轩钢结构结点刚度退化时,结构基频减小,振动形式由上部八角亭的振动转变为八角亭下部承重工字钢梁柱的局部振动,且各工况的振动方向以水平向振动为主。

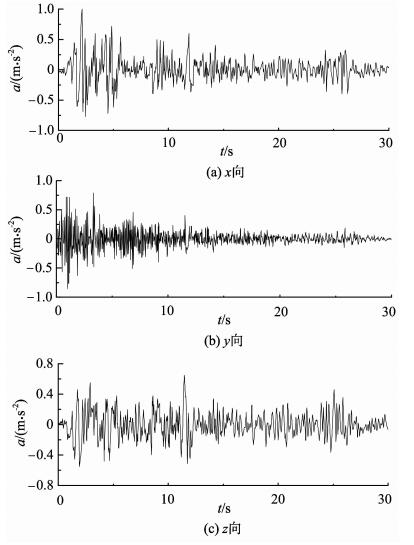
采用时程分析法研究灵沼轩钢结构在常遇地震作用下的响应情况。时程分析法的优点在于其计算结果能相对真实地反映结构的地震响应^{[21, 22]}。故宫所在地为8度抗震设防,所处场地类别为Ⅱ类,设计地震分组为第1组,且灵沼轩属甲类建筑,综合上述因素,选取x、y、z向1940年El-Centro波作用于灵沼轩,截取前30 s时段,时间间隔0.02 s,各个方向的加速度峰值略大于《建筑抗震设计规范》(GB 50011-2010) 中表 5.1-2-2的规定值(0.07g,g为重力加速度,g=9.8 m/s²),x向取值为PGA=0.1 g,x∶y∶z=1.00∶0.85∶0.65,地震波曲线详图 7。此外,结构的阻尼比为0.04。

图 7(Fig. 7)

图 7 El-Centro波曲线 Fig. 7 Curves of El-Centro waves

基于模态分析结果,选取以下代表性节点来研究灵沼轩钢结构的位移和加速度响应情况:1-4-F位置的柱子裂缝位置 (节点编号3 716),八角亭顶部位置(节点编号3 289),工字钢框架顶部位置(节点编号241)。选取以下代表性节点研究灵沼轩钢结构的内力响应情况:3 716号节点及支撑八角亭的工字钢梁跨中位置(节点编号1 443),研究弯矩响应情况;工字钢框架前侧柱根位置 (节点编号81),研究剪力响应情况;上述节点所在位置详见图 3。

进行分析时,结构的强度及变形容许值参考文献[18, 23, 24],从保守角度考虑取值,工字钢梁的抗拉、压、弯强度[f_y1]=300 MPa,抗剪强度[f_yv1]=170 MPa;铸铁柱及八角亭的抗拉、压、弯强度[f_y2]=544 MPa,抗剪强度[f_yv2]=90 MPa;结构的水平向容许变形值的[Δ_ue]=[θ_e]h=h/250=0.0137 m,其中h为计算层层高,h=3.43 m。

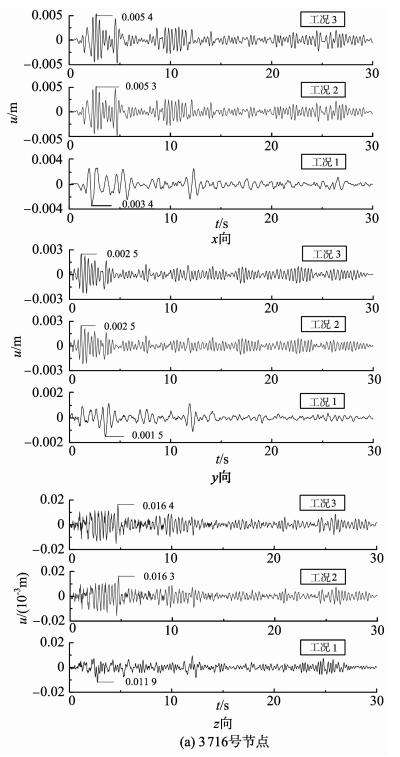
地震作用下,节点3 716、3 289位移响应曲线见图 8。节点241位移响应峰值见表 5。节点位移响应曲线特点:(1) 各曲线以平衡位置为中心,保持近似均匀振动,反映了地震作用下结构保持稳定振动状态;(2)工况2、3条件下,节点位移响应曲线形状基本相同,反映了节点刚度由10³数量级退化到0时,节点位移响应变化不明显。

图 8(Fig. 8)

图 8 3 716号与3 289号节点位移响应曲线 Fig. 8 Displacement response curves of nodes 3 716 and 3 289

表5(Table 5)

表5 节点241位移峰值 Table 5 Peak displacement values of node 241 节点 位移响应峰值/m 工况1 工况2 工况3 x向 0.007 4 0.008 1 0.008 1 y向 0.002 8 0.003 8 0.003 9 z向 2.04×10-5 2.55×10-5 2.58×10-5

表5 节点241位移峰值 Table 5 Peak displacement values of node 241

地震作用下,节点位移响应峰值特点:(1) 对节点3 716及241而言,工况2条件下的位移响应峰值大于工况1;而对于节点3 289而言,工况2的节点位移响应远小于工况1。结合模态分析结果,可知工况1、2条件下,结构的振动形式发生明显改变。当承重钢框架结点刚度由10⁶数量级退化到10³数量级时,其振动形式由八角亭的振动改为承重框架的局部振动。节点3 716及241属于位于承重钢框架上,当节点刚度退化时,其振动表型明显;而节点3 289位于八角亭上,当刚度退化时,其振动减弱。(2) 对各节点而言,工况3条件下节点的位移响应峰值与工况2差别很小。不难发现,其主要原因在于墙体对承重钢框架提供了充足的约束,在结点刚度由工况1退化到工况2后,墙体约束条件对结构振动起主导作用。以至于承重钢框架结点刚度由10³数量级退化到0时,节点的位移响应峰值及振动曲线形状变化不明显。 (3) 不同工况条件下,节点241(一层顶部)及节点3 289(二层顶部)的水平位移响应峰值均在容许范围内。另由于节点3 716为开裂位置,该位置位移响应峰值很小,因此可以认为,开裂并未造成裂缝处位置产生过大变形。

不同工况条件下,各节点的加速度响应峰值见表 6。各节点加速度响应峰值的特点:(1)随着节点位置增高,工况1条件下,各节点在x、y、z三个方向加速度响应峰值增大,这说明地震作用下,结构加速度响应随着高度增加有放大现象;工况2、3条件下,节点3 289的加速度响应峰值反而小于节点241。这是因为节点3 289位于八角亭顶部,而节点241位于工字钢框架顶部;工况1条件下,结构振动以八角亭的水平振动为主,地震波沿结构高度方向容易放大;而工况2、3条件下,结构振动形式以下部承重框架的局部振动为主,上部八角亭受到的振动影响不大。(2)与工况1相比,工况2和工况3条件下,同一节点的加速度响应峰值变化不大。这反映了承重钢框架的结点刚度退化到一定程度时,墙体对承重框架的约束对结构的振动形式起主要控制作用,结构加速度响应的变化不再明显。 (3)对同一节点而言,与工况1条件相比,工况2、3加速度响应峰值减小,可反映结点刚度产生退化时,结构因地震作用产生破坏的可能性不大。(4)与其它节点相比,节点3 716在各工况条件下的加速度峰值并无明显突出,反映了该开裂位置产生的地震作用力并不过大。

表6(Table 6)

表6 节点加速度响应峰值 Table 6 Peak acceleration values of nodes 方向 节点 加速度响应峰值/(m·s-2) 工况1 工况2 工况3 3 716 0.920 0.290 0.370 x向 241 1.960 1.430 1.440 3 289 2.310 1.130 1.100 3 716 1.710 1.250 1.230 y向 241 1.910 1.270 1.270 3 289 2.160 1.120 1.110 3 716 0.087 0.028 0.029 z向 241 0.089 0.040 0.041 3 289 0.121 0.023 0.021

表6 节点加速度响应峰值 Table 6 Peak acceleration values of nodes

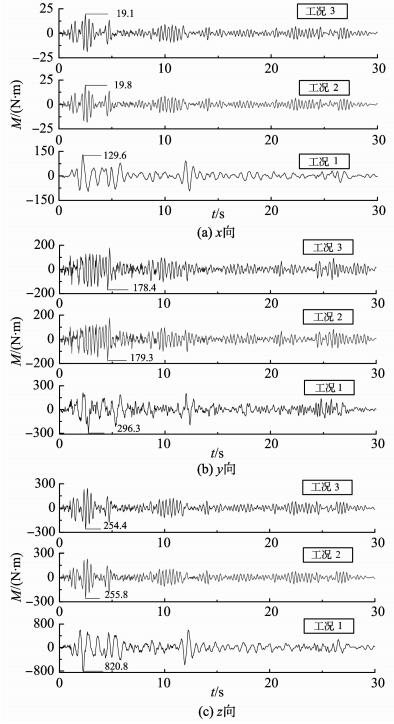
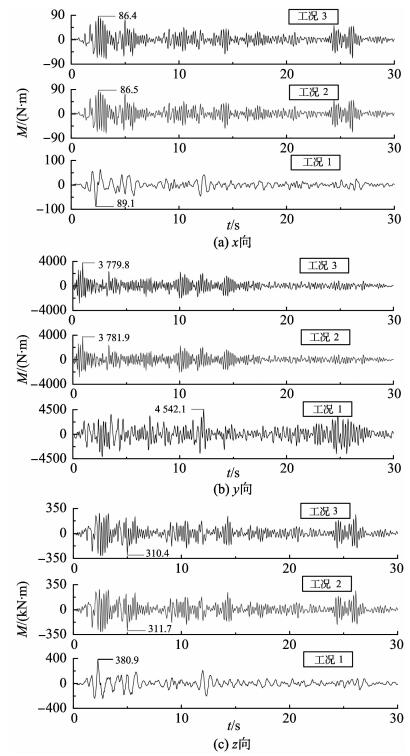
3 716及1 443号节点属于承重框架,其弯矩响应曲线见图 9、10。分析可知工况1条件下,各节点的弯矩响应峰值大于工况2、3,且工况2、3的弯矩响应情况类似。其主要原因在于工况2、3条件下结构的振动形式相近,且与工况1条件差别明显。采取平方和平方根法对x、y、z向的弯矩值进行组合,获得工况1条件下3 716号节点弯矩峰值845.4 N·m,对应截面的弯应力峰值为50.6 MPa<[f_y2],即开裂柱不会产生弯曲破坏;工况1条件下1 443号节点的弯矩组合值为4 545.8 N·m,对应截面的弯应力峰值为4.4 MPa<[f_y1],即指定工字钢梁不会产生弯曲破坏。

图 9(Fig. 9)

图 9 3 716号节点弯矩响应曲线 Fig. 9 Bending moment response curves of node 3 716

图 10(Fig. 10)

图 10 1 443号节点弯矩响应曲线 Fig. 10 Bending moment response curves of node 1 443

81号节点位于承重框架柱根位置,其剪力响应曲线见图 11。分析可知结点刚度退化条件下,该节点的剪力响应峰值有所减小,但表现不明显;工况2、3条件下,该节点的剪力响应曲线特征相似。另采取平方和平方根方法组合后,可得该节点的剪力响应峰值为660.0 N。依据剪应力相关计算公式,可得相应截面的剪应力峰值为2.4 MPa<[f_yv2]。由此可知,结点刚度退化时,钢结构框架的上述典型结点内力响应趋于减弱,其主要原因在于结构的振动形式发生改变。

图 11(Fig. 11)

图 11 81号节点剪力响应曲线 Fig. 11 Shear force response curves of node 81

根据文献[12]中“5.5 抗震变形验算”相关规定,分别考虑不同工况,分析8度罕遇地震作用下灵沼轩钢结构的薄弱层变形情况,以评价结构的抗倒塌能力。响应谱分析法取代耗时的时间域瞬态分析,可以快速地近似获得结构的峰值响应^{[25, 26]}。本研究采用单点响应谱分析方法对灵沼轩钢结构进行抗震性能分析。响应谱为x、y、z 3个方向同时施加,强度比例仍为x∶y∶z=1.00∶0.85∶0.65。谱分析参数与文献[12]相同,x向地震影响系数最大值α_max=0.9,特征周期T_g=0.35 s,阻尼调整系数η₂=1,地震影响曲线下降段的衰减指数γ=0.9,曲线下降段斜率调整系数η₁=0.02。

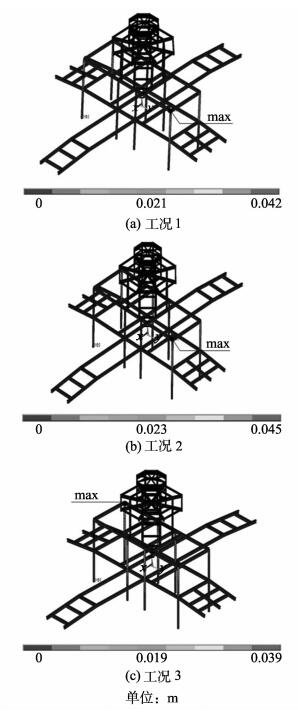
基于以上分析假定,获得3种工况条件下位移峰值见表 7,其中|u_max|表示结构位移峰值,|u|层间位移峰值,钢结构的整体变形分布见图 12。分析可知:各工况条件下结构的薄弱层为2层,最大值均发生在梁柱节点位置,且工况3条件下的|u|值最大,|u|=1/123。由于文献[12]规定罕遇地震作用下钢结构薄弱层的容许相对变形为1/50,因此可以认为3种工况条件下,灵沼轩钢结构均不会产生倒塌。其主要原因与灵沼轩充足的支撑点密切相关。

表7(Table 7)

表7 8度罕遇地震作用下结构位移结果 Table 7 Displacement results of the structure under 8-degree intensity of earthquakes |umax|/m |u|/m |u|/h 工况 1 0.042 0.025 1/137 工况 2 0.045 0.026 1/132 工况 3 0.039 0.028 1/123

表7 8度罕遇地震作用下结构位移结果 Table 7 Displacement results of the structure under 8-degree intensity of earthquakes

图 12(Fig. 12)

图 12 8度罕遇地震作用下钢结构变形分布 Fig. 12 Displacement distributions of the steel structures under 8-degree intensity of rare occurred earthquakes

本研究基于钢结点刚度退化影响,考虑不同工况条件,对故宫灵沼轩钢结构开展动力特性与地震响应研究,得出以下结论:

(1) 灵沼轩承重钢框架结点刚度退化时,结构基频减小,振动形式由上部八角亭的振动转变为八角亭下部承重工字钢梁柱的局部振动,且各工况的振动方向以水平向振动为主。

(2) 8度常遇地震作用下,结构在不同工况条件下均能保持稳定振动状态。

(3) 8度常遇地震作用下,典型节点(含开裂最严重位置)的变形及内力响应峰值均在容许范围内,可反映钢结构具有较好抗震性能。

(8) 8度罕遇地震作用下,不同工况条件下的钢结构均有较好的抗倒塌能力。

(4) 结点刚度退化时,工字梁—铸铁柱框架部分变形响应峰值趋于偏大,而内力响应峰值趋于偏小,其主要原因在于结构的振动形式产生变化。

与已有相关成果相比,本研究侧重讨论了考虑了节点刚度退化的钢结构动力特性及抗震性能,其结果不仅深化了钢结构的研究内容,而且可对钢结构文物建筑的保护提供理论参考。后续工作应开展结构动力特性实测及钢节点力学性能相关试验,以获得灵沼轩钢结构动力特性与地震响应较全面的成果。