2.烟台大学经济管理学院, 山东 烟台 264005
2. School of Economy and Management, Yantai University, Yantai 264005, Shandong, China
旅行商问题(traveling salesman problem,TSP)是著名的组合优化问题,在物流业快速发展的今天,对于快递公司确定便捷合理的邮递路线具有重要的意义。TSP得到了广泛的研究,其求解方法大体可分为精确求解和启发式求解两种[1]。精确求解方法[2]难以求出大型TSP实例的最优解,而启发式方法能在可接受的时间内给出近似最优解,因此得到很多关注[3, 4, 5, 6]。启发式求解又包括构造方法和提升方法等,构造方法在最初的回路上逐步增加新顶点,最终得出哈密顿回路;提升方法针对一个可行解进行改进,以期得出更好解。二者混合的方法对最初构造的回路进行改进,提升解的质量[1]。APPLEGATE D等在1999年提出了Tour Merging,先找到一些较好解,并假定最好解的边已经出现在这些较好解中。合并所有较好解的边集,在只含有这些边的图中搜索长度最小的哈密顿回路[7],算法属于图搜索算法。康立山等提出的基于构建基因库求解TSP的遗传算法,由最小生成树建立TSP的基因库,保存最有希望成为最优解上的边[8],算法有一定随机性。申铉京等提出快速蚁群算法求解TSP,计算蚁群算法得到的最优解和次优解之间的公共路径,认为这些公共路径会出现在最优解中[9],但是随着问题规模的增大,这个假设可能不再成立。集成学习(ensemble learning)使用多个学习机来解决同一问题,能显著提高一个学习系统的能力,在机器学习界得到了广泛关注[10]。周志华等人提出了“选择性集成(selective ensemble)”的概念,认为使用中小规模的集成即可获得较好效果[11]。文献[12]对选择性集成学习算法进行了综述,按照某种衡量准则从所有的基分类器中选出一些分类器,以降低时间和空间要求并提高分类精度。选择性集成可用于分类、聚类等问题的求解[13, 14, 15, 16],文献[13]根据各基分类器的混淆矩阵构造基分类器间相关性矩阵,基于该矩阵选择基分类器参与集成,最后融合所选基分类器的决策结果;文献[14]中通过计算互补指数对候选分类器进行排序,使用动态选择与循环集成算法选出最优分类器子集;文献[15, 16]将集成方法用于谱聚类,构造多样的谱聚类成员,并给出选择性集成聚类结果。另外,选择性集成还成功应用于网络流的特征选择[17]和磨机负荷参数建模[18]等。
本研究采用选择性集成的思想,给出了一种混合型启发式算法来求解TSP。对于一个TSP实例,首先构造出一个回路,然后利用2-opt算子进行提升,给出更好的解。主要贡献为:(1)将选择性集成思想用于TSP求解,提出了扩大路径法来构造属于最优解的一段或几段路径。与已有文献不同的是,算法对较好解的边进行投票,不是图搜索算法;按照扩大路径法生成几个极大路径,不是直接求较好解之间的公共路径。(2)算法在参与集成的较好解确定的情况下给出确定的解,没有不确定性。(3)重新定义2-opt邻域,将寻找TSP最优解转化为寻找其2-opt邻域内的解。
1 旅行商问题与2-opt 1.1 旅行商问题旅行商问题通常用图的方式描述,设G=〈V,E,C〉是边带权的完全图,其中V={v1,v2,…vn}是顶点集合,E={(vi,vj)|vi,vj∈V,vi≠vj}是边集合,C=[c(vi,vj)]是权值向量(距离矩阵),c(vi,vj)表示边(vi,vj)的长度或者代价。G的哈密顿回路是指通过G中所有顶点一次且仅一次的回路,回路的长度定义为回路上边的长度之和。TSP寻找长度最小的哈密顿回路H*,即
| $c\left({{H^*}} \right)=\mathop {\min }\limits_H \sum\limits_{\left({{v_i},{v_j}} \right)\in H} {c\left({{v_i},{v_j}} \right).} $ | (1) |
考虑对称TSP,即对于任意的vi,vj,c(vi,vj)=c(vj,vi)。将哈密顿回路简称为线路。
1.2 2-exchange与2-opt设H=v1,v2,…vn,v1是一条线路,对于两个顶点vi,vj,2-交换(2-exchange)是指将线路中不相邻的两条边(vi,vi+1)和(vj,vj+1)换成(vi,vj)和(vi+1,vj+1),得到一条新线路[1]。如果c(vi,vi+1)+c(vj,vj+1)-c(vi,vj)-c(vi+1,vj+1)>0,则2-交换得到的线路是对原线路的改进。
定义1称一个线路是2-opt(2-optimal)局部最优解,是指不能通过2-交换将当前线路进一步缩短长度[1]。
定义2获取一个2-opt局部最优解的过程称为2-opt方法。2-opt方法反复采用2-交换对给定线路H进行改进,直到新线路不能再通过2-交换改进为止,此时的新线路记作2-opt(H)。
定义3设有n个城市,H是一个2-opt局部最优解,S是所有可能线路集合,则H的2-opt邻域定义为可以经2-opt方法找到H的线路集合:
| ${N_{{\rm{2opt}}}}\left(H \right)=\left\{ {{H_1} \in S:{2_{{\rm{ - opt}}}}\left({{H_1}} \right)=H} \right\}.$ |
文献[1]中定义的2-opt邻域是指一个可行解H经过一次2-交换可以得到的可行解集合,H是2-交换的起始点,因此文献[1]中的2-opt邻域可以看作是H的2-opt后继集。定义的2-opt邻域是针对一个2-opt局部最优解H的,H是一系列2-交换的终点,这里的2-opt邻域是能通过2-opt方法找到H的解集合,因此定义的2-opt邻域可以看作是H的2-opt前驱集。
如果线路H*是该TSP的最优解,则寻找最优解的问题就转化为寻找N2opt(H*)的问题了。如果能找到该邻域内的一个元素,就等于找到了最优解。通过试验发现,寻找N2opt(H*)的元素并不容易。对于5个TSP实例分别进行200次试算,都没有发现最优解。但是根据优势分析结果,每个2-opt试算结果仍优势于至少O((n-2)!)个可行解[19],因此是较好解。
2 算法设计2-opt方法简单有效,经常应用于需要确定最优回路的组合问题中,因此采用2-opt方法作为提升回路质量的手段。将{1,2,…,n}的随机排列作为试算线路输入2-opt方法,得出的线路好于输入线路。对这些较好线路采用选择性集成策略,提出了扩大路径法来构造若干条极大路径。使用顶点插入法将剩余顶点和这些极大路径连接起来,构造出最初的线路H,希望H能出现在N2opt(H*)中。最后利用2-opt方法进行提升改进,给出最终线路。算法的流程图如图 1所示。
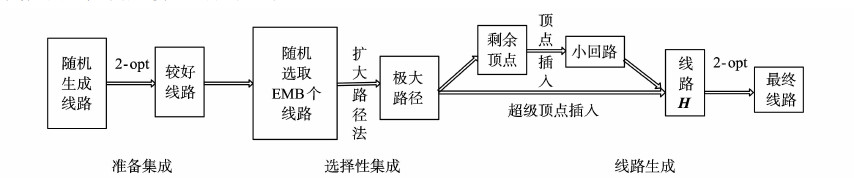
|
图1 算法流程图 Fig. 1 Algorithm flow chart |
采用选择性集成思想,对于一个TSP实例,预先获取若干个较好解,每个解相当于一个专家,通过专家对各边的投票,确定各边属于最优线路的可能性。对各边投票的结果进行有选择的采用,以期发现属于最优解的一段或几段路径。
算法1 选择性集成
输入:TSP的距离矩阵c,2-opt方法试算得出的所有较好线路集合T,参与集成的线路数EMB,阈值位置pos;
输出:若干条极大路径的集合P;
(1)各边的投票数vote清0。
(2)从T中随机选取EMB个线路,每条线路t对所经过的边e=(vi,vj)进行投票:
| $vote\left({{v_i},{v_j}} \right)\leftarrow vote\left({{v_i},{v_j}} \right)+1.0c\left({{v_i},{v_j}} \right).$ |
(3)将各边投票数按从小到大排序,得到有序的投票序列v,重复的数值只保留一次。
(4)阈值thrd=v(round(length(v)*pos));%阈值为序列v的指定位置处的值。
(5)现有路径P清空。
(6)找出vote的最大值,记作g。
(7)while g>=thrd
{①将投票值等于g的边e=(x,y)按扩大路径法插入现有路径:
(a)如果x,y都不曾出现在现有路径中,如图 2(a),则新建一条路径(x,y);
(b)如果x,y中有一个(例如x)是现有路径的端点,另一个(y)不曾出现在现有路径中,如图 2(b),则将y与x连接;
(c)如果x,y分别是两个路径的端点,如图 2(c),则将两个路径连接成一个路径;
(d)其余情况不再扩大路径,如图 2(d)。
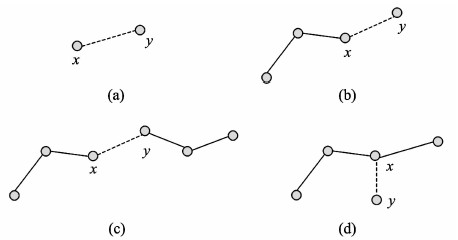
|
图2 扩大路径法 Fig. 2 Expanding path method |
②将边e的投票值清0。
③找出vote的最大值,仍记作g;}
(8)返回极大路径的集合P。
算法1的运行时间与参数的关系见试验分析。
在算法1步骤(2)中,线路t对所经过的边的投票值不是简单加1,因为一条较长的边出现在最优线路上的可能性较小,因此线路的有效投票值应该用边的长度进行校正。算法的步骤(4)设定参与构建路径的边的投票阈值,该阈值是随着TSP实例和参与集成的线路的不同而不同的,因此需要动态确定阈值。从算法1步骤(7)可以看出,参与构建极大路径的边是投票值大于阈值的边,这些边按投票值由大到小的顺序参与构建路径,考虑了集成学习中对该边属于最优线路的信任程度。那些投票值较小的边,不符合大多数参与投票者的意向,因此不予考虑。
算法1结束后返回若干个彼此不交的路径,这些路径按照算法1不能再扩展了,因此称之为极大路径。这些极大路径不一定会覆盖所有的顶点,因此需要设计算法将剩余顶点和这些极大路径连接起来,生成一个线路。
2.2 线路生成设经过扩大路径法得到k个极大路径p1,p2,…,pk,剩余m个点vi1,vi2,…,vim没有出现在任何极大路径上。采用顶点插入法将vi1,vi2,…,vim构成一个长度为m的小回路Cm,图 3给出顶点插入法示意图。首先取3个顶点vi1,vi2,vi3构成一个回路C′,如果m <3,则构成环(m=1)或者两条平行边(m=2)。然后将其余顶点逐个插入当前回路中,如图 3(a)所示。选择回路C′的边(vl,vl+1),使得在边(vl,vl+1)上插入顶点vis时,(2)式达到最小。
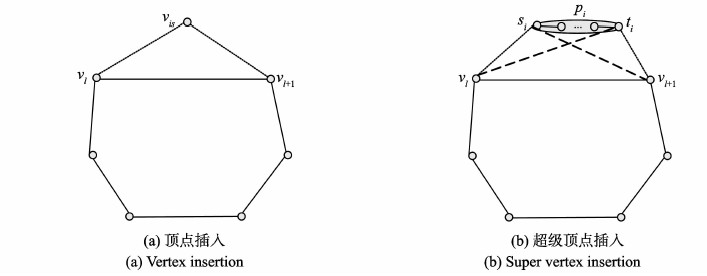
|
图3 顶点插入法 Fig. 3 Vertex insertion algorithm |
| $c\left({{v_l},{v_{is}}} \right)+c\left({{v_{is}},{v_{l+1}}} \right)- c\left({{v_l},{v_{l+1}}} \right).$ | (2) |
当vi1,vi2,…,vim插入完毕时,得到一个长度为m的小回路Cm。根据优势分析的结果,顶点插入法得到的回路Cm的优势数是O((m-2)!),因此这样构造的小回路是m个点的哈密顿回路中的较好解[20]。
以下将极大路径插入到小回路Cm中。由于极大路径是由专家投票得出的,认为其整体会出现在最优解路径上,因此将极大路径当成一个点,参加后面的顶点插入法。为了和一般的顶点区分,称为超级顶点。仍按顶点插入法将各超级顶点插入小回路。超级顶点可能调整放置方式,但在回路中并不展开,确保在后续的构造中不被破坏。如图 3(b)所示。
算法2 超级顶点插入法
输入:极大路径p1,p2,…pk,TSP的距离矩阵c,小回路Cm
输出:线路H
(1)依次处理每个极大路径p1,p2,…pk。i=1;H=Cm。
(2)设极大路径pi的两个端点为si,ti,记作pi=[si,ti],其长度记为Len(pi)。
(3)考虑H的每条边el=(vl,vl+1):%注:将pi=[si,ti]插入回路H中
①如果vl,vl+1是普通顶点,则计算
| $\begin{array}{l} c\left({{v_l},{p_i}} \right)+c\left({{p_i},{v_{l+1}}} \right)- c\left({{v_l},{v_{l+1}}} \right)- \\ \min \left\{ {c\left({{v_l},{p_i}} \right)+c\left({{t_i},{v_{l+1}}} \right)+{\mathop{\rm len}\nolimits} \left({{p_i}} \right),c\left({{v_l},{t_i}} \right)+c\left({{s_i},{v_{l+1}}} \right)+{\mathop{\rm len}\nolimits} \left({{p_i}} \right)} \right\} - c\left({{v_l},{v_{l+1}}} \right). \end{array}$ | (3) |
②如果vl是超级顶点vl=[ul,rl],则(3)式中c(vl,si)=c(rl,si),c(vl,ti)=c(rl,ti)。
③如果vl+1是超级顶点,则(3)式中c(si,vl+1)和c(ti,vl+1)的计算类似。
(4)选取使(3)式取最小值的边el,将pi按(3)式取最小值时的放置方式插入el,即pi=[si,ti]或pi=[ti,si]。更新回路H,i=i+1,回到2,直到所有极大路径处理完毕。
(5)返回H。
至此,图 1中算法的各步骤均以设计完成,下面需要实例验证。
3 试验与结果分析使用的机器CPU为Intel(R)Core(M)i5-3210M,主频2.50 GHz,4 G内存。测试TSP实例来自TSPLIB(http://www.iwr.uni-heidelberg.de/groups/comopt/software/TSPLIB95/tsp/),各实例信息如表 1所示。
| 表1 TSP实例的基本信息 Table 1 Basic information of TSP instances |
其中,EU-2是欧几里得距离,对计算出的结果取整。ATT是一种距离函数,其计算方法是:设两个点分别是zi=(xi,yi)和zj=(xj,yj),则
| $ATT\left({{z_i},{z_j}} \right)=\left\lceil {\sqrt {\left({{{\left({{x_i} - {x_j}} \right)}^2}+{{\left({{y_i} - {y_j}} \right)}^2}} \right)/10.0} } \right\rceil $ |
试验步骤1获取较好解,准备集成:
(1)以eil51为例,随机生成200个{1,2,…,51}的排列,每个排列看作是一个可行解。对每个可行解进行2-opt提升,共得到200个较好解,各个解的最小值min、最大值max、平均值mean、方差var见表 2,均值与方差已取整。表 2中同时列出其余TSP实例的较好解情况,其中Pr76(1)和Pr76(2)是Pr76的两组较好解,每组均包含200个解。
| 表2 各实例的较好解分组 Table 2 High quality solution groups for instances |
(2)试验步骤2选择性集成与线路生成
集成大小EMB定义为参加集成的可行解个数,初步试验表明EMB太小(如10)或太大(如200)都不能得出较好的结果,因此设定EMB=40和50进行如下试验。
如前所述,thrd是投票阈值,当一条边的投票阈值≥thrd时,此边将参与构建极大路径。试验中取投票值队列(从小到大排序)的位置pos=1/5,1/4,1/3,1/2处的投票值作为thrd的取值。
集成得出的解如果不理想,可以尝试提高参加集成的解的质量。如Pr76当参加集成解的质量提高到19 000以下时(如解分组Pr76(2)),就有最优解稳定出现。如表 3所示。
| 表3 集成算法在两组Pr76上的结果 Table 3 Comparison of the ensemble algorithm on two groups for Pr76 |
试验参数只包含EMB和pos两个参数,每组参数组合重复试验50次,对50次结果进行统计,得到表 4所示结果。对于两个较小的实例Eil51和Pr76,在8种参数设置下均能找到最优解。随着实例规模的增加,8种参数设置下找到的最优解与TSPLIB解的偏差也在缓慢增加,规模到达1 400个城市时,偏差仍小于1.7%。在选择性集成的研究中,通常会注意参与集成的成员精度和成员多样性,本算法先获取较好解分组来保证参与集成的解的精度,并没有直接要求解的多样性。因为从试验中发现,同一个TSP的两个解即使线路长度相差很小,其解的形态也能相差甚远,即构成两个线路的边集合有很大差别,这个多样性是TSP自身具备的,因此文中没有特别强调集成的多样性问题。从试验结果中没有发现最优解出现的一致参数设置,但在集成大小EMB=50,pos=1/3~1/4处算法在各实例上均有较好表现。
| 表4 集成算法在5个实例上的最好结果及与TSPLIB解的偏差(50次运行) Table 4 The best outcome and bias of the ensemble algorithm on 5 instances (50 runs) |
图 4给出了集成算法在fl1400上的运行时间(指在一组参数下获取一个解的平均时间)与EMB和pos的关系。随着pos的加大,满足投票阈值的边数下降,集成算法的运行时间减少,运行时间与pos呈近似线性关系。EMB是参与集成的可行解数量,EMB从40增加到50时,算法运行时间略有增加。
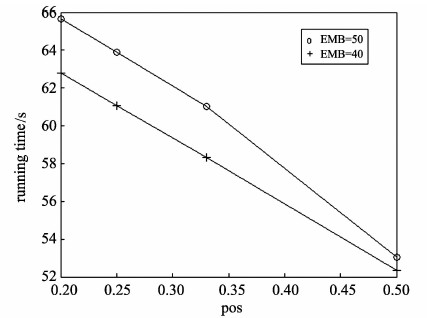
|
图4 集成算法在fl1400上的运行时间 Fig. 4 Running time of the ensemble algorithm on fl1400 |
选择性集成算法有选择地利用高质量解提供的部分信息,可以有效地提高学习质量,曾在各种学习任务中成功应用。尝试将选择性集成思想应用到TSP中,通过各较好解对边的投票,选出参加集成的边,再利用扩大路径法直接给出极大路径,并辅以2-opt方法对结果进行提升。2-opt邻域的定义使得一个解(最好解)的搜索转化为多个解(2-opt邻域内的解)中的任何一个解的搜索,降低了搜索难度。未来的工作中会进一步吸收启发式学习的新思想,尝试将其应用到TSP的求解中,在计算时间和空间受限情况下,提高对大规模组合优化问题的求解能力。
| [1] | REGO C, GLOVER F. Local search and metaheuristics[M]. New York: Springer Science+Business Media, 2007:309-368.( 5) 5) |
| [2] | DANTZIG G B, FULKERSON D R, JOHNSON S M. Solution of a large-scale traveling-salesman problem[J]. Operations Research, 1954, 2(4):393-410.( 1) 1) |
| [3] | LIN S, KERNIGHAN B W. An effective heuristic algorithm for the traveling salesman problem[J]. Operations Research, 1973, 21(3):972-989.( 1) 1) |
| [4] | 吴斌,史忠植.一种基于蚁群算法的TSP问题分段求解算法[J].计算机学报,2001,24(12):1329-1333.WU Bin, SHI Zhongzhi. An ant colony algorithm based partition algorithm for TSP[J]. Chinese Journal of Computers, 2001, 24(12):1329-1333.( 1) 1) |
| [5] | 孟佳娜,王立宏.具有自识别能力的遗传算法求解旅行商问题[J].计算机工程与应用,2006,42(13):51-53.MENG Jiana, WANG Lihong. A genetic algorithm with self-identify capability to solve TSP[J]. Computer Engineering and Applications, 2006, 42(13):51-53.( 1) 1) |
| [6] | 孟佳娜,王立宏.基于组织调整的进化算法求解TSP问题[J].计算机工程与应用,2006,42(12):57-59.MENG Jiana, WANG Lihong. Evolutionary algorithm based on organization adjustment to solve TSP[J]. Computer Engineering and Applications, 2006, 42(12):57-59.( 1) 1) |
| [7] | APPLEGATE D, BIXBY R, CHVATAL V, et al. Finding tours in the TSP[R]. Bonn: University of Bonn, 1999.( 1) 1) |
| [8] | 杨辉,康立山,陈毓屏.一种基于构建基因库求解TSP问题的遗传算法[J]. 计算机学报,2003,26(12):1753-1758.YANG Hui, KANG Lishan, CHEN Yuping. A gene-based genetic algorithm for TSP[J]. Chinese Journal of Computers, 2003, 26(12):1753-1758.( 1) 1) |
| [9] | 申铉京,刘阳阳,黄永平,等. 求解TSP问题的快速蚁群算法[J]. 吉林大学学报(工学版),2013,43(1):147-151.SHEN Xuanjing, LIU Yangyang, HUANG Yongping, et al. Fast ant colony algorithm for solving traveling salesman problems[J]. Journal of Jilin University(Engineering and Technology Edition), 2013, 43(1):147-151.( 1) 1) |
| [10] | DIETTERICH T. Machine learning research: four current directions[J]. AI Magazine,1997, 18(4):97-136.( 1) 1) |
| [11] | ZHOU Z H, WU J X, TANG W. Ensembling neural networks: many could be better than all[J]. Artificial Intelligence, 2002, 137(1-2):239-263.( 1) 1) |
| [12] | 张春霞, 张讲社. 选择性集成学习算法综述[J]. 计算机学报, 2011, 34(8):1399-1410.ZHANG Chunxia, ZHANG Jiangshe. A survey of selective ensemble learning algorithms[J].Chinese Journal of Computers, 2011, 34(8):1399-1410.( 1) 1) |
| [13] | 毕凯,王晓丹,姚旭,等. 一种基于Bagging和混淆矩阵的自适应选择性集成[J]. 电子学报,2014, 42(4):711-716.BI Kai, WANG Xiaodan, YAO Xu, et al. Adaptively selective ensemble algorithm based on bagging and confusion matrix[J]. Acta Electronica Sinica, 2014, 42(4):711-716.( 1) 1) |
| [14] | 郝红卫,王志彬,殷绪成,等. 分类器的动态选择与循环集成方法[J].自动化学报,2011, 37(11):1290-1295.HAO Hongwei, WANG Zhibin, YIN Xucheng, et al. Dynamic selection and circulating combination for multiple classier systems[J]. Acta Automatica Sinica, 2011, 37(11):1290-1295.( 2) 2) |
| [15] | JIA J H, XIAO X, LIU B X, et al. Bagging-based spectral clustering ensemble selection[J]. Pattern Recognition Letters, 2011, 32:1456-1467.( 2) 2) |
| [16] | WANG L H, WANG X L. Eigenvectors selection for spectral clustering based on semi-supervised selective ensemble[J]. Journal of Computational Information Systems, 2014, 10(9):3701-3710.( 2) 2) |
| [17] | 潘吴斌,程光,郭晓军,等. 基于选择性集成策略的嵌入式网络流特征选择[J]. 计算机学报,2014,37(10):2128-2138.PAN Wubin, CHENG Guang, GUO Xiaojun, et al. An embedded feature selection using selective ensemble for network traffic[J]. Chinese Journal of Computers, 2014, 37(10):2128-2138.( 1) 1) |
| [18] | 汤健,柴天佑,丛秋梅,等. 基于EMD和选择性集成学习算法的磨机负荷参数软测量[J]. 自动化学报,2014, 40(9):1853-1866.TANG Jian, CHAI Tianyou, CONG Qiumei, et al. Soft sensor approach for modeling mill load parameters based on EMD and selective ensemble learning algorithm[J]. Acta Automatica Sinica, 2014, 40(9):1853-1866.( 1) 1) |
| [19] | PUNNEN A, MARGOT F, KABADI S. TSP heuristics: domination analysis and complexity[J]. Algorithmica, 2003, 35:111-127.( 1) 1) |
| [20] | GUTIN G, YEO A. Exponential neighborhoods and domination analysis for the TSP[M]. New York: Springer Science+Business Media, 2007: 223-256.( 1) 1) |



