K-Means算法是一种广泛应用的聚类算法。它的初始聚类中心点是随机选择的,这给聚类结果带来了很大的不确定性[1]。TZORTZIS G等人提出了一种基于最大最小距离法寻找初始聚类中心的方法[2];ZHANG Y J等人利用数据点之间的邻近相似度来确定数据点的相似密度,选择密度大的数据点作为初始聚类中心[3];MA G W等人利用聚集度函数和层次聚类来确定初始聚类中心[4];JOSHI K D等人通过计算类中每个数据样本之间的最大最小距离求出密度最大的数据样本作为初始聚类中心[5];YUAN F等人根据聚类对象分布密度来确定初始聚类中心[6];HAN L等人根据聚类对象分布密度来确定初始聚类中心[7];HE Y X等人通过融合相关性高的子类,逐渐优化子类再确定初始聚类中心[8];王玲等人提出一种密度敏感的相似性度量,将其引入谱聚类得到密度敏感的谱聚类算法[9];钱线等人提出初始化K-Means的谱方法[10];张靖等人提出了基于个体轮廓系数自适应地选取优秀样本以确定初始聚类中心的改进算法[11];XU J等人提出了基于RNN(reverse nearest neighbor)的选取算法[12];孙秀娟等人提出基于密度和距离的初始中心点优化算法[13]。MOORE A等人提出一种基于kd树的数据结构来存储样本间距离信息的K-Means算法[14]。ASHA G K等人提出基于模糊聚类的K-Means改进算法(AGK)[15]。重复从数据集中选取熵最小的样本放入初始聚类中心集合中,并从数据集中删除该样本及与该样本相似的样本,直到数据集中无数据为止。SATHIYA G等人提出了K-Means改进算法(SG)[16],该算法是通过计算每个样本到原点的距离,根据这个距离对样本进行排序,再将得到的排序结果等分成K个数据子集,用每个数据子集中排序居中的那个样本作为初始聚类中心。NAZEER K A A等人提出了K-Means改进算法(NKAA)[17],该算法首先计算每个样本与其他样本的距离,找出距离值最小的2个样本,将它们放入Am(1≤m≤k)子集中,并将这2个数据点从数据集中移除,再从数据集中找出离Am子集距离最小的样本放入Am中,并将其从数据集中移除。重复这一操作,直到Am子集中样本的数量达到预先设定的阈值。最后通过计算每个子集中样本的均值,将这些均值作为K-Means的初始聚类中心。与传统K-Means算法相比,这些算法在一定程度上提高了聚类结果的准确率,但迭代次数较多。
为了能够在提高聚类结果准确率的同时减少算法的迭代次数,提出一种基于薛定谔方程的K-Means算法(K-Means clustering algorithm based on the Schrödinger equation,S-K-Means),利用薛定谔方程中的势能函数的最小值能表示类中心这一特性来确定初始聚类中心点,通过优化初始聚类中心提高聚类结果的准确率并减少算法的迭代次数。
1 K-Means算法K-Means聚类算法[18],以K为输入参数,把N个对象分为K个类。算法的主要处理流程如下:首先随机选择K个对象分别作为1个类的初始聚类中心。把剩余的每个对象划分到距离最近的1个类中。然后再重新计算每个新类的类中心。重复这个过程,直到准则函数收敛。通常采用均方误差作为准则函数,其定义如下:
| $E={\sum\limits_{i=1}^k {\sum\limits_{p \in {c_i}} {\left| {p - {m_i}} \right|} } ^2},$ | (1) |
其中:E表示的是数据集中所有对象的均方误差和;p表示1个对象;mi表示类Ci的类中心。
K-Means聚类算法中的距离计算采用欧氏距离来确定。欧氏距离的定义如下:
| $\begin{array}{l} d\left({x,j} \right)=\\ \;\;\;\;\;\sqrt {{{\left({{x_{i1}} -,{x_{j1}}} \right)}^2}+{{\left({{x_{i2}} -,{x_{j2}}} \right)}^2}+\ldots {{\left({{x_{in}} -,{x_{jn}}} \right)}^2}}, \end{array}$ | (2) |
其中,i=(xi1,xi2,…,xin)和j=(xj1,xj2,…,xjn)是2个n维数据对象。
2 基于薛定谔方程的K-Means算法 2.1 薛定谔方程薛定谔方程是由奥地利物理学家薛定谔提出的一个量子力学的基本方程[19],量子力学描述的是微观粒子在量子空间的分布情况。薛定谔方程的表达如下:
| $H \cdot \varphi \left(x \right)=\left({ - \frac{{{\sigma ^2}}}{2}{\nabla ^2}+p\left(x \right)} \right)\varphi \left(x \right)=E \cdot \varphi \left(x \right),$ | (3) |
其中:σ为方差;H为Hamilton算子;E为H的能量特征值;▽是拉普拉斯算子;φ(x)为波函数;p(x)是势能函数。
波函数φ(x)是粒子量子态的描述[20],波的强度能反映出粒子出现在空间某处的概率的大小,φ(x)的最大值表示量子集中出现的区域的中心。对于1个普通的数据集来说,φ(x)的最大值表示的就是数据集中类的中心。
薛定谔方程具有对偶性,即φ(x)的最大值对应了p(x)的最小值。由于φ(x)很容易受σ值的影响,σ的细微变化会使φ(x)发生巨大变化。而p(x)对σ具有一定的鲁棒性,σ可以在一个较大的区间变化,p(x)都可以给出较为准确的类中心。因此为了提高聚类结果的稳定性,这里直接对p(x)最小值进行计算,用它来表示数据集中类的中心。
通过对薛定谔方程的原形进行求解得到p(x)为
| $P\left(x \right)=E+\frac{{{\sigma ^2}}}{{2\varphi \left(x \right)}}{\nabla ^2}\varphi \left(x \right),$ | (4) |
这里,波函数φ(x)用经验分布函数来代替,经验分布函数的表达式如下:
| $\varphi \left(x \right)=\sum\limits_i {{e^{ - \left\| {x - {x_i}} \right\|}}^{{{^{2/2}}^{{\sigma ^2}}}}},$ | (5) |
那么就有
| $P\left(x \right)=E - \frac{n}{2}+\frac{1}{{2{\sigma ^2}}} \cdot \frac{{\sum {_i{{\left\| {x - {x_i}} \right\|}^2}{{\rm{e}}^{{ - ^{ - \left\| {x - {x_i}} \right\|}}^{{{^{2/2}}^{{\sigma ^2}}}}}}} }}{{\sum {_i{{\rm{e}}^{{ - ^{ - \left\| {x - {x_i}} \right\|}}^{{{^{2/2}}^{{\sigma ^2}}}}}}} }},$ | (6) |
其中,n是数据维数。假设p(x)为非负数,那么E便可表示为
| $E=- min\frac{{{\sigma ^2}}}{{2\varphi \left(x \right)}}{\nabla ^2}\varphi \left(x \right),$ | (7) |
针对1个观测样本集合{x1,x2,…,xn},此时对p(x)的计算便构成了1个{p(xi)}的序列
| $P\left({{x_i}} \right)=E - \frac{n}{2}+\frac{1}{{2{\sigma ^2}}} \cdot \frac{{\sum {_i{{\left\| {{x_i} - {x_j}} \right\|}^2}{{\rm{e}}^{ - \frac{{{{^{ - \left\| {{x_i} - {x_j}} \right\|}}^{^2}}}}{{^{2{\sigma ^2}}}}}}} }}{{\sum {_i{{\rm{e}}^{ - \frac{{{{^{ - \left\| {{x_i} - {x_j}} \right\|}}^{^2}}}}{{^{2{\sigma ^2}}}}}}} }},$ | (8) |
在量子力学中,微观粒子在空间中的分布情况与粒子本身所具有的势能密切相关,粒子在空间里的分布情况取决于空间中的势能,随着粒子的势能趋近于0或比较小时,它周围所吸附的粒子数目也会越多。对于聚类算法而言,一个类的中心点周围也应该吸附着更多的数据点。量子力学中所研究的微观粒子在空间中的分布情况与聚类算法中数据样本的分布情况十分类似,因此可以利用量子力学的这一原理来确定聚类的中心点。本研究提出的S-K-Means算法正是利用这一原理来确定初始聚类中心,具体步骤如下:
(1)首先计算每个数据样本的p(x)值并将数据集按照p(x)值进行升序排序;
(2)设定距离阈值,用各个对象之间的平均距离作为距离阈值;
(3)将p(x)值最小的样本放入初始聚类中心集合中并将其从数据集中删除;
(4)计算数据集中的数据样本与聚类中心集合里的所有数据样本的距离,如果与聚类中心集合里所有数据样本的距离都大于距离阈值就把该数据样本放入初始类中心集合中并将该数据样本从数据集中删掉,否则直接删除该样本;
(5)重复第4步操作,直到初始聚类中心集合中样本的数量等于所需要的聚类数量为止。
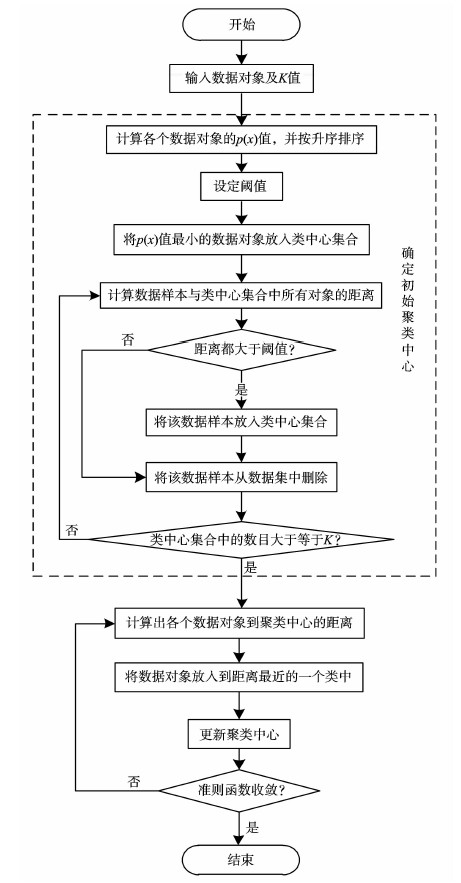
算法流程图见图 1。
|
图1 算法流程图 Fig. 1 Flow chart for proposed method |
试验硬件环境为Acer Veriton D4300 Intel(R)Core(TM)i5-3470 CPU @ 3.20GHz,4GB内存,软件环境为64位的Windows7和MatlabR2012b。
数据集采用的是UCI数据库中的Iris、Wilt、Balance Scale、Teaching Assistant Evaluation。其中,Iris包含150个数据样本,每个样本有4个属性,共有3个类,每个类包含50个数据样本;Wilt包含4889个数据样本,每个样本有6个属性,共有2个类,分别包含261、4578个数据样本;Balance Scale包含625个数据样本,每个样本有4个属性,共3个类,分别包含49、288、288个数据样本;Teaching Assistant Evaluation共有151个数据样本,每个样本有5个属性,共3个类,分别包含49、50、52个数据样本。
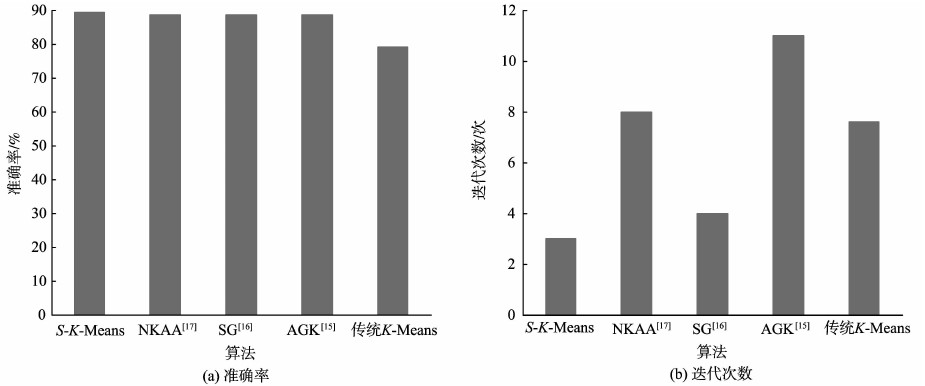
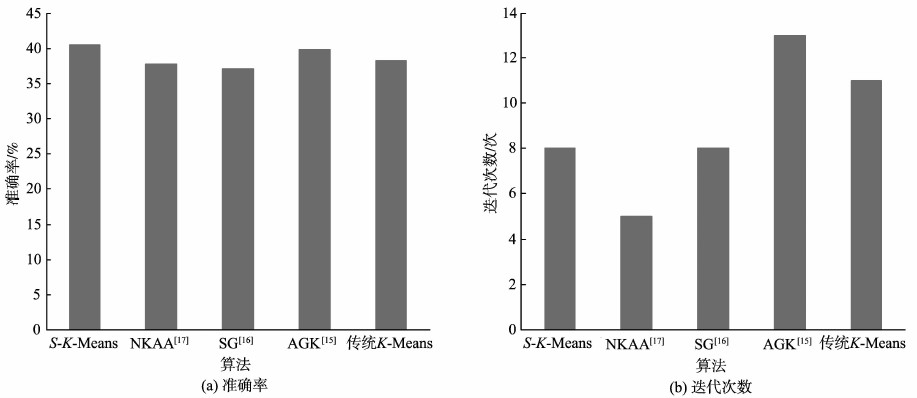
3.2 试验结果为了验证S-K-Means算法的有效性,选取传统K-Means算法、AGK[15]、SG[16]和NKAA[17]进行对比试验。传统K-Means的初始聚类中心是随机选择的,这里对传统K-Means取10次样再求平均,这里以Iris数据集为例得到10组数据,具体数据见表 1所示,其它数据集的取法与此类似。针对Iris数据集得到的试验结果见图 2;Wilt数据集得到的试验结果见图 3;Balance Scale数据集得到的试验结果见图 4;Teaching Assistant Evaluation数据集得到的试验结果见图 5。
| 表1 传统K-Means针对Iris数据集的10次取样数据 Table 1 The data of Iris 10 sampling |
|
图2 Iris数据集试验结果 Fig. 2 Results comparison chart for Iris |
|
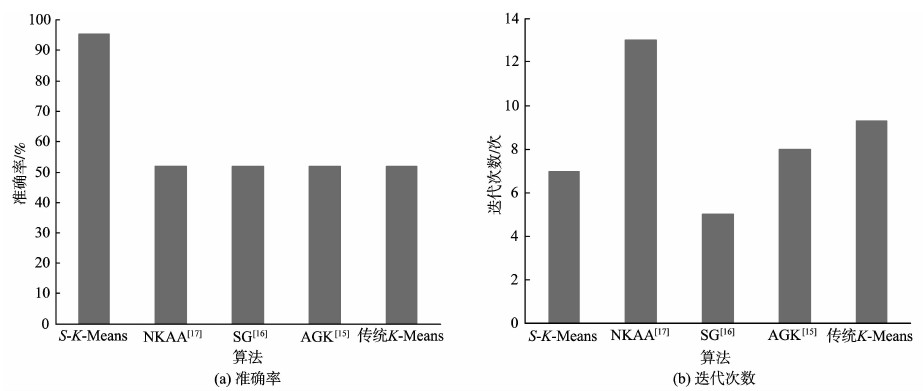
图3 Wilt数据集试验结果 Fig. 3 Results comparison chart for Wilt |
|
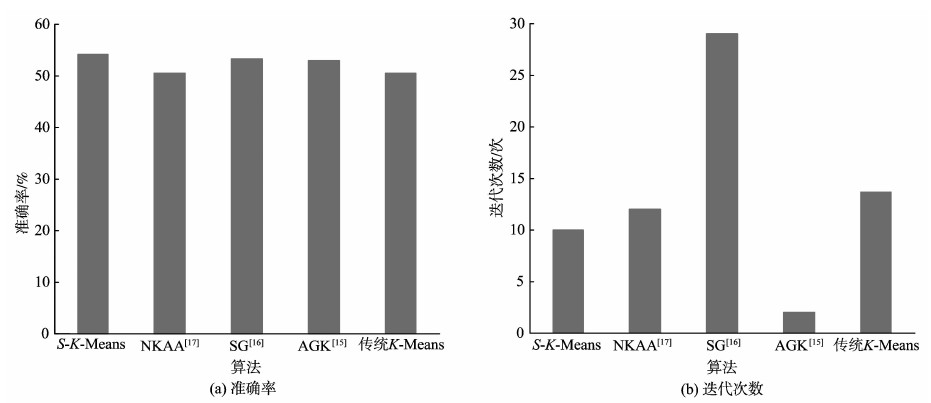
图4 Balance Scale数据集试验结果 Fig. 4 Results comparison chart for Balance Scale |
|
图5 Teaching Assistant Evaluation数据集试验结果 Fig. 5 Results comparison chart for Teaching Assistant Evaluation |
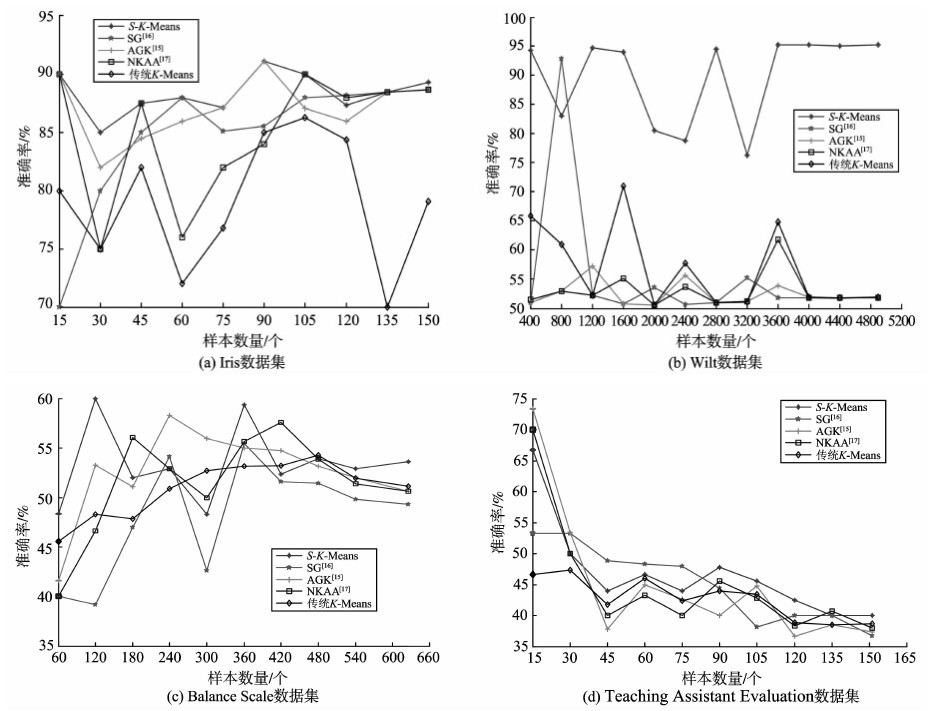
为了进一步验证本研究方法的有效性,对不完整的数据集进行试验,将数据集内的数据样本的顺序打乱,通过逐渐增加数据样本的数量,观察聚类结果的准确率,试验结果见图 6。
|
图6 数据集不完整时的试验结果 Fig. 6 Results with a different sample size |
从图 6中可以看出,所提出的算法稳定性更高,在数据集不完整的情况下,本研究方法在大多数情况下能获得更高的准确率,并且在数据集趋于完整的情况下,本研究方法能更快地趋于稳定。但是针对Wilt数据集,本研究方法的波动性还是较大,这是由于Wilt数据集所含的两类数据样本的数量差异比较大(分别包含261、4578个数据样本),这在数据集不完整的情况下就会影响试验结果的准确性。
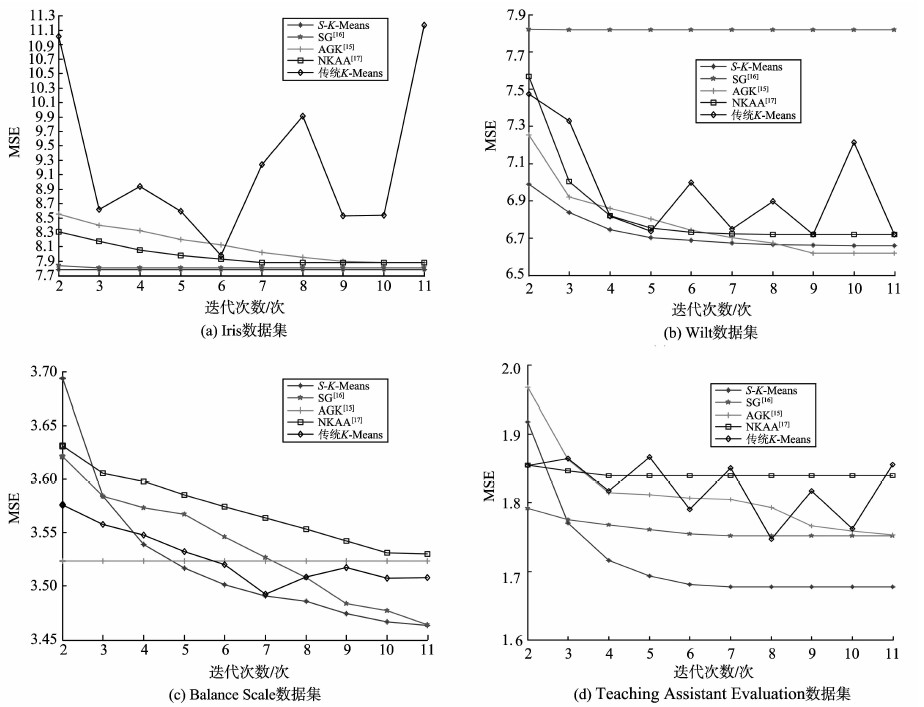
各个算法在不同迭代次数下所得到MSE(Mean Squared Error)见图 7,由于MSE的值比较大,这里对同一组所得到的试验数据进行等比例缩放。从图 7的试验结果可以看出,本研究方法在不同迭代次数下,随着迭代次数的增加能更快地取得较小的MSE值,MSE的值越小说明聚类效果越好。
|
图7 不同迭代次数所得到的MSE Fig. 7 Results with a different iteration number |
图 7的试验结果跟图 2~5基本保持一致,通过观察图 7可以看出,有的算法虽然收敛速度比较快,但是MSE值还比较大,例如图(b)中文献[16]中的算法。
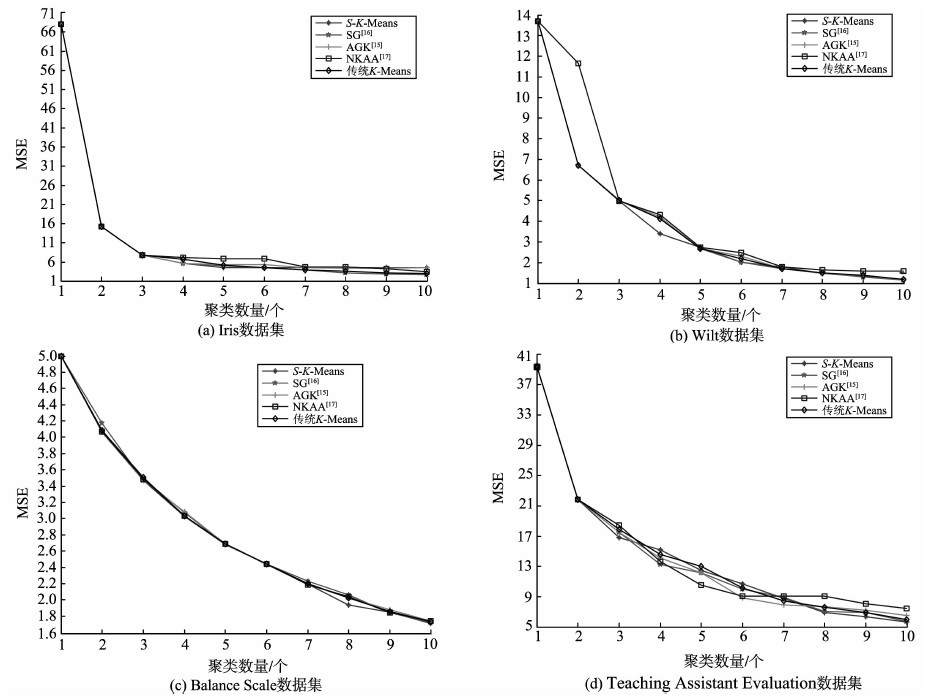
各个算法在不同聚类数量下所得到MSE(Mean Squared Error)见图 8。从图 8的试验结果可以看出,随着聚类数量的增加,几种算法所得到的MSE值比较相近,但从整体上看,本研究方法在大多数情况下能取得较小的MSE。
|
图8 不同聚类数量所得到的MSE Fig. 8 Results with a different cluster number |
通过对以上试验结果进行分析可看到,由于传统K-Means算法的初始聚类中心是随机选择的,针对同一数据集其准确率不及另外几种改进的K-Means算法。从试验结果可以看出S-K-Means算法性能优于其他几种改进算法,在提高聚类结果的准确率的同时,在多数情况下能减少算法的迭代次数。这是由于S-K-Means算法在确定初始聚类中心时不是简单地利用几何中心或随机确定,而是利用数据样本本身所具有的潜在信息来确定的。通过数据样本本身所具有的潜在信息确定的初始聚类中心将更加符合实际,这有利于目标函数更快地收敛,因此会在一定程度上减少算法的迭代次数。
4 结论针对K-Means算法初始聚类中心随机选择这一问题,提出一种基于薛定谔方程的K-Means聚类算法,利用薛定谔方程的势能函数确定初始聚类中心。通过计算样本对应的势能函数值,筛选符合要求的样本作为初始聚类中心。利用数据样本本身所具有的潜在信息来确定初始聚类中心更加符合实际,这有利于目标函数更快地收敛,从而减少迭代次数。试验证明:S-K-Means算法能有效提高聚类结果的准确率,在多数情况下能减少迭代次数。
| [1] | 汪中,刘贵全,陈恩红.一种优化初始中心点的K-means算法[J].模式识别与人工智能,2009,22(2):299-304.WANG Zhong, LIU Guiquan, CHEN Enhong. A K-means algorithm based on optimized initial center points[J]. Pattern Recognition and Artificial Intelligence, 2009, 22(2):299-304.( 1) 1) |
| [2] | TZORTZIS G, LIKAS A. The minmax k-means clustering algorithm[J]. Pattern Recognition, 2014, 47(7):2505-2516.( 1) 1) |
| [3] | ZHANG Y J, CHENG E. An optimized method for selection of the initial centers of k-means clustering[M]. Berlin, Germany: Springer, 2013: 149-156.( 1) 1) |
| [4] | MA G W, XU Z H, ZHANG W, et al. An enriched K-means clustering method for grouping fractures with meliorated initial centers[J]. Arabian Journal of Geosciences, 2014, 8(4):1881-1893.( 1) 1) |
| [5] | JOSHI K D, NALWADE P S. Modified K-Means for better initial cluster centres[J]. International Journal of Computer Science and Mobile Computing, 2013, 2(7):219-223.( 1) 1) |
| [6] | YUAN Fang, ZHOU Zhiyong, SONG Xin. K-means clustering algorithm with meliorated initial center[J]. Computer Engineering, 2007, 33(3):65-66.( 1) 1) |
| [7] | HAN L, WANG Q, JIANG Z F, et al. Improved k-means initial clustering center selection algorithm[J]. Jisuanji Gongcheng yu Yingyong(Computer Engineering and Applications), 2010, 46(17):150-152.( 1) 1) |
| [8] | HE Y X, CAI R, WU L B, et al. K-Means optimization algorithms of initial clustering center based on regional density[J]. Applied Mechanics and Materials, 2014, 513:478-482.( 1) 1) |
| [9] | 王玲, 薄列峰, 焦李成. 密度敏感的谱聚类[J]. 电子学报, 2007, 35(8):1577-1581.WANG L, BO L F, JIAO L C. Density-Sensitive spectral clustering[J]. Acta Electronica Sinica, 2007, 35(8):1577-1581.( 1) 1) |
| [10] | 钱线, 黄萱菁, 吴立德. 初始化K-means的谱方法[J]. 自动化学报, 2007, 33(4):342-346.QIAN X, HUANG X J, WU L D. A spectral method of K-means initialization[J]. Acta Automatica Sinica, 2007, 33(4):342-346.( 1) 1) |
| [11] | 张靖, 段富. 优化初始聚类中心的改进k-means算法[J]. 计算机工程与设计, 2013, 34(5):1691-1694.ZHANG J, DUAN F. Improved k-means algorithm with meliorated initial centers[J]. Computer Engineering and Design, 2013, 34(5):1691-1694.( 1) 1) |
| [12] | XU J, XU B, ZHANG W, et al. Stable initialization scheme for k-means clustering[J]. Wuhan University Journal of Natural Sciences, 2009, 14(1):24-28.( 1) 1) |
| [13] | 孙秀娟, 刘希玉. 基于初始中心优化的遗传K-means聚类新算法[J]. 计算机工程与应用, 2008, 44(23):166-168.SUN Xiujuan, LIU Xiyu. New genetic K-means clustering algorithm based on meliorated initial center[J]. Computer Engineering and Applications, 2008, 44(23):166-168.( 1) 1) |
| [14] | PELLEG D, MOORE A. Accelerating exact k-means algorithms with geometric reasoning[C]// Proceedings of the fifth ACM SIGKDD international conference on Knowledge discovery and data mining. NewYork, USA: ACM, 1999: 277-281.( 1) 1) |
| [15] | KAREGOWDA A G, VIDYA T, JAYARAM M A, et al. Improving performance of K-Means clustering by initializing cluster centers using genetic algorithm and entropy based fuzzy clustering for categorization of diabetic patients[C]// Proceedings of International Conference on Advances in Computing. Delhi, India: Springer, 2012: 899-904.( 2) 2) |
| [16] | SATHIYA G, KAVITHA P. An efficient enhanced K-Means approach with improved initial cluster centers[J]. Middle-East Journal of Scientific Research, 2014, 20(1):100-107.( 3) 3) |
| [17] | NAZEER K A A, SEBASTIAN M P. Improving the accuracy and efficiency of the k-means clustering algorithm[C]// Proceedings of the World Congress on Engineering. London, UK: IAENG, 2009, 1:1-3.( 2) 2) |
| [18] | MACQUEEN J. Some methods for classification and analysis of multivariate observations[C]// Proceedings of the fifth Berkeley symposium on mathematical statistics and probability. California, USA: University of California Press, 1967, 1(14): 281-297.( 1) 1) |
| [19] | MERCER J. Functions of positive and negative type, and their connection with the theory of integral equations[J]. Philosophical transactions of the royal society of London. Series A, containing papers of a mathematical or physical character, 1909, 209:415-446.( 1) 1) |
| [20] | GASIOROWICZ S. Quantum physics[M]. New York, USA: John Wiley & Sons, 2007.( 1) 1) |
| [21] | LICHMAN M. (2013). UCI Machine Learning Repository. Irvine, CA: University of California, School of Information and Computer Science. http://archive.ics.uci.edu/ml. |




