2. 福州大学物理与信息工程学院, 福建 福州 350116
2.College of Physics and Information Engineering, Fuzhou University, Fuzhou 350116, Fujian, China
虚拟手术系统是虚拟现实技术在现代医学领域中的应用之一。在外科虚拟手术中加入流血模拟效果能够提高手术的真实感,对于培养医生应对病人出血情况的能力具有重要的意义。由于不同手术模拟场景和操作行为会引发不同的流血现象,模拟过程既要实现血液流动的效果又要考虑医学的特性,视觉反馈的真实感和实时性也是其硬性要求,因此流血模拟也是虚拟手术中的一个难点[1]。血流真实感绘制作为虚拟手术系统中的一个重要组成部分,随着虚拟手术的进行而实时产生,其绘制的效果将直接决定虚拟手术系统的整体真实感。
作为虚拟手术系统中的关键技术之一,血流真实感绘制也得到快速的发展。近年来,国外的研究人员对血流的真实感绘制问题进行大量的研究。RIANTO S等人结合立方插值拟质点方法模拟了血液流动[2];QIN J将弹簧模型与SPH相结合实现了血液与血管的相互作用[3]; ITANI M A等人研究血液在脑动脉中的流动特性并开发一种可用于虚拟手术的脑血管血流仿真系统[4]。国内也有很多学者对血流的真实感绘制问题进行研究。黄雷、肖双九等人实现了人体内部血液流动及肿瘤表面点状出血的效果[5];施鹏、熊岳山等人提出一种结合力反馈机制的渗血模拟仿真模型[6]。邱文超等人实现血管内血液的流动以及虚拟手术过程中血管壁破裂流血特效场景[7]。从总体上来讲,尽管血流真实感绘制领域经过不断的发展,其绘制效果不断加强,但还存在着很大的改进空间[8]。这些改进空间主要体现在真实感的提升和复杂度的降低两个方面。
1 血流模拟算法的分析 1.1 SPH由LUCY L B等人于1977年提出的SPH是一种纯粹的无网格拉格朗日粒子方法,也是最早的无网格方法之一[9]。SPH使用一组粒子离散和代表所模拟的介质(流体或固体),并且基于粒子体系近似和估算介质运动的控制方程,具有无网格方法的明显特点[10]。
这里所需的基本原理是用核函数W(r-r′,h) 对δ(r-r′) 进行近似,其中h是光滑长度,mm。当W(r-r′,h) 的光滑长度h→0时,近似的误差为0,即:
| $\mathop {{\rm{lim}}}\limits_{x \to 0} W\left( {r - r',h} \right) = \delta \left( {r - r'} \right),$ | (1) |
连续函数A(r)可以写成以下形式:
| $A\left( r \right) = \int {A\left( {r'} \right)} \delta \left( {r - r'} \right){\rm{d}}r'.$ | (2) |
连续函数A(r)的离散形式如下:
| $A\left( r \right) = \sum\limits_j {{m_j}\frac{{{A_j}}}{{{\rho _j}}}W} \left( {r - r',h} \right).$ | (3) |
SPH是一种基于粒子的方法,其与质点网格方法有相似点,但是根本的差异在于SPH中计算空间导数时无需网格,而是通过核函数的积分核进行核函数估值近似,将Navier-Stokes方程组[11, 12]转换为数值计算的SPH方程。该方法使得整个流场离散成一系列的粒子,将流场中的物理量转换为粒子上承载的物理量。这些粒子可以按照流体力学的规律任意地流动。试验表明:人血与Casson模型[13, 14]具有较高的符合度,因此使用Casson模型来模拟人血的流动比较符合真实情况。SPH避免了扭曲和网格缠绕的问题,而且该算法在含真空的三维系统和缺乏对称性的计算中非常有效。这是由于将网格建立的差分方法用于三维环境中时会造成网格数目的急剧增加,另外对于真空区域的网格划分又会浪费计算机的存储量,而SPH用粒子群来模拟血流,可以克服上述两个缺点。作为一种真正的无网格法,SPH已经在若干方面展现了较大的优势。但是,将SPH应用于血液流动的数值计算中会出现以下两个问题:
(1) 将使用Casson模型约束的Navier-Stokes方程组转化为离散的形式,方程中的黏滞力项将变得异常复杂;
(2) 使用SPH时必须计算当前粒子作用域内的粒子,其计算量过大。假设在模拟过程中,使用3 000个粒子来模拟血流,那么在每一帧中,都必须计算9×106次,由此引起的计算溢出问题会降低虚拟手术的实时性和精确度。
1.3 改进SPH的分析在Casson模型的Navier-Stokes方程组动量守恒方程中,黏滞力项的形式为▽·τ 。由于剪切应力张量h 可以表示为表观黏度与切变率之间的乘积,Casson模型的表观黏度h(|${\dot \gamma } $|) 是一个与位置分布有关的量,这对于哈密顿算子[15, 16]而言不是一个常数,无法直接提到哈密顿算子的左边。这将导致Casson模型的黏滞力项中的哈密顿算子的右边是一个张量,而直接使用SPH对该项进行离散化是比较复杂的。因此,这一项会导致直接使用SPH对Casson模型的Navier-Stokes方程组进行离散变得极为复杂。为此,采用上一帧表观黏度的平均值代替当前帧的表观黏度,而上一帧的表观黏度平均值在当前帧与位置分布无关,因此可以提到哈密顿算子的左边,这使得黏滞力项的计算得以简化。简化后,能够随时间发生变化的黏度成为一个与位置信息无关的量,降低了方程组的计算量。
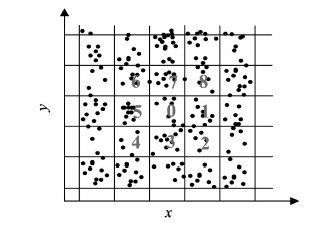
在搜索近邻粒子的问题上使用类似Euler网格[17, 18]的概念能够极大地提高运算速度。由于核函数的作用域是一个半径为h的球形区域,因此可以将流场可能覆盖的搜索区域缩小至这个球形区域的附近。使用包围该球形的立方体区域作为粒子的搜索区域。对于二维情况,首先建立一个边长为h的网格,对于区域“0”中的粒子而言,与之距离小于h的粒子必然处于区域“0”至区域“8”之间,近邻粒子搜索原理的示意图见图 1。然后对于三维情况,只需把二维中的情况拓展至三维的各个方向,因此,对于每个区域,搜索自身区域与邻近26个区域即可。
|
图1 近邻粒子搜索原理 Fig. 1 Principle of neighbor particle search |
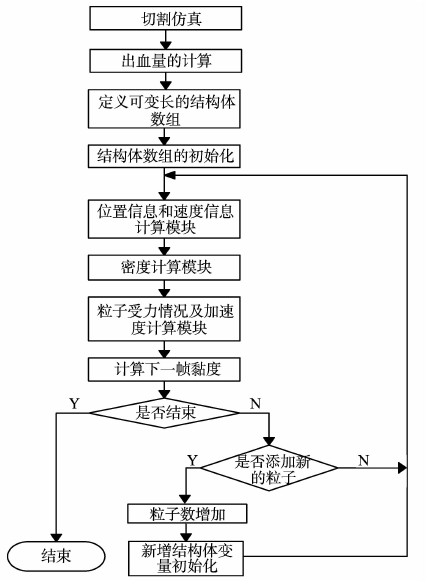
针对以上的分析,可以得出基于改进SPH的血流模拟算法的步骤,算法流程图见图 2。
|
图2 算法流程图 Fig. 2 Algorithm flow chart |
改进SPH的步骤如下:
(1) 假设将切口分成n块,根据每一块顶点坐标值计算每一小块区域的面积。根据区域面积将全部粒子分成n部分,每个部分的粒子数与区域面积成正比。整个切口的面积等于所有这些区域的面积之和,考虑出血粒子数与切口面积的关系,计算出血量。
(2) 随着计算的进行,新的粒子不断地从伤口处产生,这就要求表示血流的结构体数组的长度必须是可变的,选用指向结构体类型变量的指针来定义可变长结构体数组。
(3) 根据真实的手术切口流血情况可知,切口较深位置的出血量一般比较多,切口较浅处的出血量比较少。因而,结构数组的初始化中,初始位置根据切口形状进行均匀分布,其后新产生的粒子也由该分布进行初始化
。(4) 根据血粒子上一帧的加速度ai 计算新一帧的速度uinew 并根据uinew 计算新一帧的位置xinew 的公式:
| $u_i^{{\rm{new}}} = {u_i} + {a_i} \cdot \Delta t,$ | (4) |
| $x_i^{{\rm{new}}} = {x_i} + u_i^{{\rm{new}}} \cdot \Delta t,$ | (5) |
其中,Δt为两帧间隔的时间,s。通过计算帧率f来计算当前这一秒内的平均间隔时间,使用平均间隔时间来近似代替Δt,二者的关系如下:
| $\Delta t \approx \frac{1}{f}.$ | (6) |
本研究设计了一个函数CalculateFrameRate()计算帧率f,其主要思想是设计一个表示时间间隔的变量和一个帧数累加器framesPerSecond,通过main函数每帧对其调用一次,每次调用该函数都会对framesPerSecond进行累加,当时间间隔超过1 s时,记录framesPerSecond的数值并清0。
(5) 根据近邻粒子对该粒子密度的贡献值计算粒子的密度。近邻粒子的寻找方法是根据当前粒子近邻粒子搜索编号,得到近邻粒子的编号要求。根据1.3节提到的近邻粒子搜索原理,将粒子i的近邻粒子搜索编号记为(Nx,Ny,Nz) ,则该粒子的近邻粒子编号需处于附近27个编号之一。
(6) 当遍历所有近邻粒子后,粒子受力情况需要补充重力项。由于当前粒子的密度已由计算得知,因此可以直接将密度与重力加速度矢量相乘得到重力项的3个分量,从而得出每个粒子所受的3个力,再利用动量守恒方程的简化形式得到粒子的加速度。
(7)采用上一帧表观黏度的平均值作为当前帧的黏度近似值。因此,在计算粒子受力情况之前需要对黏度进行计算,然后存放在一个全局变量中,最后粒子在计算受力情况时就只需调用全局变量的值即可。本研究所使用的黏度是表观黏度的平均值,因而必须先求出各个位置上的黏度值。根据表观黏度的公式可知,欲求表观黏度,首先要求出切变率 的第二不变量|${\dot \gamma } $| 。根据|${\dot \gamma } $| 的计算公式,可以发现,|${\dot \gamma } $| 与速度分布有关。
因此,必须计算 $\frac{{\partial u}}{{\partial x}}$ 、 $\frac{{\partial u}}{{\partial {\rm{y}}}}$ 、 $\frac{{\partial u}}{{\partial z}}$ 、 $\frac{{\partial v}}{{\partial x}}$ 、 $\frac{{\partial v}}{{\partial y}}$ 、 $\frac{{\partial v}}{{\partial z}}$ 、 $\frac{{\partial w}}{{\partial x}}$ 、 $\frac{{\partial w}}{{\partial y}}$ 、 $\frac{{\partial w}}{{\partial z}}$ 这9个变量值。
在SPH计算中,雅可比矩阵▽u [19]可以通过以下的公式计算:
| $\nabla {u_i} = \sum\limits_j {\frac{{{m_j}}}{{{\rho _j}}}\left( {{u_j} - {u_i}} \right)} \otimes \nabla W\left( {{r_i} - {r_j},h} \right),$ | (7) |
得到雅可比矩阵▽u后即可计算出上述9个量,从而计算出该粒子位置上的切变率第二不变量和表观黏度。
3 仿真试验及结果分析在移动工作站(2.8 GHz Intel处理器,4.0 G内存,NVIDIA QuadroFX 770M显卡,显存 512 M)上利用标准OpenGL图形库建立仿真模型。为了直观地展示计算结果,将计算结果绘制于场景中,从而观测粒子的运动规律。
(1) 单粒子运动情况展示
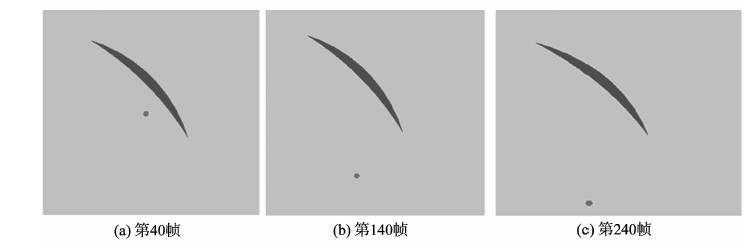
使用绘制标志位将80号粒子设置为绘制,80号以外的粒子设置为不绘制。该粒子第40帧、第140帧、第240帧的位置示意图见图 3。
|
图3 编号为80的粒子不同帧的位置 Fig. 3 The positions of different frames of the No.80 particle |
(2) 多粒子运动情况展示
将所有粒子的绘制标志位设置为绘制。为了保证试验效果具有一定的清晰度,伤口用深灰黑色进行渲染,血粒子用灰色进行渲染。第40帧至第65帧的血粒子由伤口向外扩散的过程见图 4,可见粒子正在由切口向外扩散,这与真实的手术中血液流动方向相符合。

|
图4 皮肤表面出血效果图 Fig. 4 Simulation results of skin surface bleeding |
(3) 本研究算法效果与其他算法效果的对比
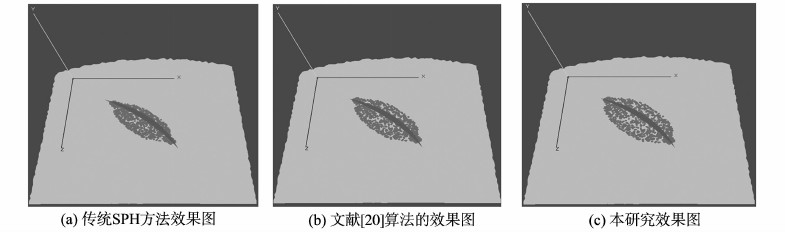
不同方法合成的皮肤表面出血效果对比图见图 5。在相同的条件下(湿度、温度、血粒子数量值均相同)进行仿真试验,通过与传统SPH方法和文献[20]所提出的算法进行比较可以看出,本研究算法得到的合成效果更加清晰地反映了血液流动的情况,与真实场景比较吻合。
|
图5 不同方法合成的皮肤表面出血效果图对比 Fig. 5 Comparison of simulation results of skin surface bleeding by using different methods |
不同的方法在血流仿真上的效率分析见表 1,本算法的帧率近似为传统SPH方法的3倍、文献[20]算法的1.5倍;消耗的内存近似为传统SPH方法的1/4,文献[20]算法的近1/3。因此,本算法能够快速模拟皮肤表面的血液流动,在保证逼真度的前提下比其它算法具有明显的速度优势,表明本算法能够满足虚拟手术中皮肤表面出血仿真的实时性要求。
| 表1 不同的方法在血流仿真上的效率分析 Table 1 Analysis of the efficiency of different methods inblood flow simulation |
在虚拟手术中,血流效果伴随着手术中的每一次切割而频繁产生,因此血流真实感绘制是大部分系统必须实现和研究的技术,其真实感将极大地影响虚拟手术系统总体的真实感。由于传统血流真实感绘制中使用牛顿流体模型近似模拟血液流动现象存在着精度不高、计算量大的局限性,通过对血液流变性质进行分析,将更加符合血液流动现象的Casson模型引入血流真实感绘制中,本研究利用相邻两帧之间黏度差别很小的特点,使用表观黏度的平均值代替当前帧的黏度值,从而使得SPH方法可以将使用Casson模型约束的Navier-Stokes方程组转化为离散的形式,降低计算的复杂度。
| [1] | 赖颢升. 虚拟手术中流血效果模拟研究[D]. 济南:山东大学, 2014. LAI Haosheng. Study of bleeding simulation in virtual surgery[D]. Jinan: Shandong University, 2014.(  1) 1) |
| [2] | RIANTO S, LI L. Fluid dynamic visualisations of cuttingsbleeding for virtual reality heart beating surgery simulation[C]//Proceedings of the 33rd Australasian Conference on Computer Science. Darlinghurst, Australia: Australian Computer Society, 2010:53-60.( 1) 1) |
| [3] | QIN J, PANG W M, NGUYEN B P, et al. Particle-based simulation of blood flow and vessel wall interactions in virtual surgery[C]//Proceedings of the 2010 Symposium on Information and Communication Technology. New York, USA: ACM, 2010:128-133.( 1) 1) |
| [4] | ITANI M A, Schiller U D, Schmieschekb S, et al. An automated multiscale ensemble simulation approach for vascular blood flow[J]. Journal of Computational Science, 2015(9):150-155.( 1) 1) |
| [5] | 黄雷,肖双九, 顾力栩, 等. 虚拟手术训练系统的血流模拟[J]. 计算机应用与软件,2011,28(1):65-68. HUANG Lei, XIAO Shuangjiu, GU Lixu. Blood flow simulation in virtual surgery training system[J]. Computer Applications and Software, 2011, 28(1):65-68.(  1) 1) |
| [6] | 施鹏, 熊岳山, 徐凯, 等. 虚拟肝脏手术中实时动态渗血效果模拟[J]. 计算机应用, 2013, 33(10): 2911-2913. SHI Peng, XIONG Yueshan, XU Kai, et al. Dynamic and real-time errhysis effect simulation in virtual liver surgery[J].Journal of Computer Applications, 2013, 33(10):2911-2913.(  1) 1) |
| [7] | 邱文超, 黄敏, 鲍苏苏, 等. 虚拟手术中血流特效场景 仿真的研究[J]. 计算机应用与软件, 2014, 31(5):46-49,162. QIU Wenchao, HUANG Min, BAO Susu, et al. Study on blood flow effects scene simulation in virtual surgery[J]. Computer Applications and Software, 2014, 31(5): 46-49,162.(  1) 1) |
| [8] | 郑广超. 虚拟手术系统中模拟手术场景的渲染和平台 的构建[D]. 上海: 上海交通大学, 2008. ZHENG Guangchao. Simulation rendering of surgical scene and platform construction in virtual surgery system[D]. Shanghai: Shanghai Jiao Tong University, 2008.(  1) 1) |
| [9] | 杨秀峰, 刘谋斌. 光滑粒子动力学SPH方法应力不稳定性的一种改进方案[J]. 物理学报, 2012, 61(22):255-262. YANG Xiufeng, Liu Moubin. Improvement on stress instability in smoothed particle hydrodynamics[J]. Acta Physica Sinica, 2012, 61(22):255-262.(  1) 1) |
| [10] | 刘谋斌, 宗智, 常建忠. 光滑粒子动力学方法的发展与应用[J]. 力学进展, 2011, 41(2):217-234. LIU Moubin, ZONG Zhi, CHANG Jianzhong. Developments and applications of smoothed particle hydrodynamics[J]. Advances in Mechanics, 2011, 41(2):217-234.(  1) 1) |
| [11] | LASIECKA I, TRIGGIANI R. Stabilization to an equilibrium of the Navier—Stokes equations with tangential action of feedback controllers[J]. Nonlinear Analysis: Theory, Methods & Applications, 2015, 121:424-446.( 1) 1) |
| [12] | PEARSON J W. Preconditioned iterative methods for Navier—Stokes control problems[J]. Journal of Computational Physics, 2015, 292:194-207.( 1) 1) |
| [13] | AKBAR N S. Influence of magnetic field on peristaltic flow of a Casson fluid in an asymmetric channel: application in crude oil refinement[J]. Journal of Magnetism and Magnetic Materials, 2015, 378:463-468.( 1) 1) |
| [14] | PONALAGUSAMY R, SELVI R T. A study on two-layered model (Casson—Newtonian) for blood flow through an arterial stenosis: axially variable slip velocity at the wall[J].Journal of the Franklin Institute, 2011, 348(9):2308-2321.( 1) 1) |
| [15] | KOMECH A, KOPYLOVA E. On eigenfunction expansion of solutions to the hamilton equations[J]. Journal of Statistical Physics, 2014, 154(1-2):503-521.( 1) 1) |
| [16] | MEHDI J, YUSUF Y. Rotation in four dimensions via generalized Hamilton operators[J]. Kuwait Journal of Science, 2013, 40(1):67-79.( 1) 1) |
| [17] | QIN Ruibin, KRIVODONOVA L. A discontinuous Galerkin method for solutions of the Euler equations on Cartesian grids with embedded geometries[J]. Journal of Computational Science, 2013, 4(1-2):24-35.( 1) 1) |
| [18] | WANG Qiuju, REN Yuxin. An accurate and robust finite volume scheme based on the spline interpolation for solving the Euler and Navier—Stokes equations on non-uniform curvilinear grids[J]. Journal of Computational Physics, 2015, 284:648-667.( 1) 1) |
| [19] | LIEDEKERKE P V, SMEETS B, ODENTHAL T, et al. Solving microscopic flow problems using Stokes equations in SPH[J]. Computer Physics Communications, 2013, 184(7):1686-1696.( 1) 1) |
| [20] | CEBRAL J R, LOHNER R. Efficient simulation of blood flow past complex endovascular devices using an adaptive embedding technique[J]. IEEE Transaction on Medical Imaging, 2005, 24(4):468-476.( 3) 3) |



