时间序列挖掘通过对时间序列进行分析处理,以期从中发现隐含的有用信息。目前,时间序列挖掘的研究主要包括时间序列的模式表示、相似性度量和搜索、聚类和分类、异常检测、预测等,其中,时间序列的相似性度量和搜索是时间序列挖掘工作的基础[1]。由于时间序列具备高维、高噪声、动态以及大规模特性,其挖掘代价很高。
目前,许多学者提出用于时间序列挖掘的各种算法。BERNDT D J和CLIFFORD J引入动态时间弯曲距离(dynamic time warping,DTW)来计算时间序列的距离,取得了令人满意的效果[2]。KEOGH E等人先后提出了LB-Keogh和LB-PAA下界算法[3, 4],以简化DTW距离计算过程,降低时间复杂度。但是,现有的计算能力依然无法满足需求,海量高维时间序列的挖掘成为一个难点。
云计算通过网络将消耗大量资源的复杂运算分布到多节点上,以获取强大的计算能力和存储能力,适应了海量数据挖掘的需求。作为新一代高性能的海量数据分布式计算平台,云平台以分布式并行计算为基础,为高维海量数据的挖掘提供了新的解决思路。丁静等人提出了云计算环境下的数据挖掘服务模式[5],杨来等人分析了基于Hadoop云平台的并行数据挖掘方法[6],证明了云计算提高数据挖掘效率的可行性。程苗提出一种基于云计算的Web数据挖掘方法[7],陈光鹏等人实现了一种基于Hadoop云计算平台的频繁闭项集并行挖掘算法[8],田国会等人将云计算与机器人学相结合[9],其使用云计算的策略实现具体应用,取得了较好的结果。
为进一步提高挖掘效率,以较小代价实现大规模时间序列数据的处理和分析,将时间序列挖掘算法与云计算相结合,提出基于Map/Reduce的时间序列相似性搜索算法。
1 基于Map/Reduce的时间序列相似性搜索时间序列的相似性搜索,是在海量时间序列中寻找与给定序列相似度最高的序列,主要内容包括全序列搜索和子序列搜索两方面[10, 11]。通常,查询目标往往是长序列中的一部分,因此,子序列搜索更具有意义。子序列相似性搜索的时间复杂度通常为O(n2m)(n为时间序列长度,m时间序列数)[12],针对其运算效率低、消耗时间长的问题,采用并行计算的方式实现子序列搜索,提出基于Map/Reduce的时间序列相似性搜索。
1.1 时间序列相似性搜索算法相似性搜索的关键在于相似性度量方法和下界过滤算法,好的相似性度量方法能够保证准确地找到最相似的序列,而高效的下界过滤算法可以大幅度简化运算过程,减少开销,降低时间复杂度。虽然学者们不断提出新的距离度量方法和下界距离[13, 14, 15, 16],但传统的动态时间弯曲距离和THAN-AWIN Rakthanmanon等人使用的LB-PAA算法仍然是适用性较高的算法[17]。
1.1.1 子序列搜索定义1 (时间序列)一组按照时间取得的数据构成的一个有序数列,
| $T={t_1},{t_2},\ldots,{t_m},$ | (1) |
其中tm为时间序列T中第m个值。
由于时间序列源数据的量级往往会很高,在实际研究中通常取其片段,即子序列,分别进行处理。
定义2 (子序列)时间序列T的子序列Ti,k表示为
| ${T_{i,k}}={t_i},{t_{i+1}},\ldots,{t_{i+k - 1}},1 \le i \le m - k+1,$ | (2) |
其中:k为子序列长度;i为子序列在原始序列中的起始位置。
假设用C表示Ti,k,用Q表示比对的标准序列。子序列搜索的目标是搜索原始序列T中与Q最相似的子序列C,如图 1所示。

|
图1 子序列搜索 Fig. 1 Subsequence search |
子序列相似性搜索包括以下步骤:
(1)对原始序列进行归一化预处理,使搜索序列与参考序列具有可搜索性;
(2)使用多维索引框架构建滑动窗口,取得原始搜索序列的子序列,并为其建立索引;
(3)使用下界算法进行过滤,将符合要求的子序列存入候选集中;
(4)最后遍历最终候选集,求每一条子序列与参考序列的DTW距离,得到最终搜索结果。子序列搜索的实现代码如下:
算法1 子序列搜索
SubsequenceMatching(Q,C,d)
for each subsequence S of C (FRM)
if LB-SW(S,Q)>d (EA)//EA表示
Early Abandon算法
break;
else LB-SW(S,Q)≤d (EA)
Add S to Candidate Set H;
end
end
for each Hi of H
if DTW(Hi,Q)<Dmin(EA)
Dmin=DTW(Hi,Q)
end
end
1.1.2 DTW距离动态时间弯曲距离最初使用在语音识别领域,该方法采用动态规划的方式计算距离,支持一对多校准,具有很好的鲁棒性。研究人员将DTW距离引入时间序列挖掘,在面对不等长或时间轴发生弯曲的时间序列时,该方法取得较好的效果[18, 19, 20]。
采用DTW距离度量时间序列相似度时,首先要构建一个m×n的矩阵D,m和n分别表示两序列的长度,矩阵中点Di,j表示qi与cj的欧氏距离。在矩阵D中,由连续的点构成一条弯曲路径P,表示两条序列相应点对齐,则计算DTW距离的首要目标为寻找最佳的弯曲路径。两条时间序列的弯曲路径必须以矩阵对角元素为起始和结束,相邻元素必须是连续的,构成弯曲路径的元素必须是单调的。
为简化运算,降低时间复杂度,在计算DTW距离时,通常采用全局约束对弯曲路径作限制。最常用的全局约束包括Sakoe-Chiba Band和Itakura Parallelogram[21],前者将弯曲路径控制在一个以对角线为轴的条状区域之内,而后者将弯曲路径控制在一个菱形区域内。
1.1.3 下界算法采用DTW距离计算时间序列的相似度,其时间复杂度为O(n2)(n为时间序列长度),运算量大,对CPU造成极大的负担。因此,研究人员提出下界距离算法,构造下界函数对明显不可能是最佳匹配的运算进行修剪,以降低CPU负担[22]。KEOGH E与Ratanamahatana C A.将时间弯曲路径全局约束的策略引入下界距离算法中[3],提出了LB-Keogh算法。
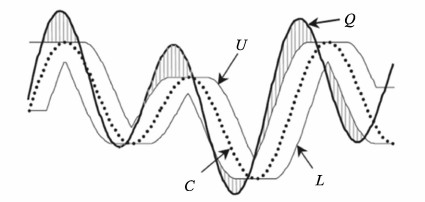
定义3 (LB-Keogh上下边界)在全局约束|i-j|≤r下(r为弯曲半径常量),对时间序列C,按照以下方式定义两条新的时间序列U、L,即为LB-Keogh算法中的上下边界曲线,
| ${U_i}=\max \left\{ {{c_{i - r}},\ldots,{c_{i+r}}} \right\},$ | (3) |
| ${L_i}=\min \left\{ {{c_{i - r}},\ldots,{c_{i+r}}} \right\},$ | (4) |
其中,U是时间序列C中长度为2r+1窗口中的最大值。相反,L是时间序列C中长度为2r+1窗口中的最小值。U与L形成一个包含序列C的信封,如图 2所示。
|
图2 LB-Keogh边界曲线 Fig. 2 The boundary curve of LB-Keogh |
定义4(LB-Keogh下界距离)查询序列Q位于信封外的点到U、L的欧氏距离之和为LB-Keogh下界距离,用Dlb-Keogh(C,Q)表示。
| ${D_{{\rm{lb\_Keogh}}}}\left({C,Q} \right)==\sqrt {\mathop \sum \limits_n^{i=1} \left\{ {\begin{array}{*{20}{c}} {{{\left({{q_i} - {u_i}} \right)}^2},}\\ {{{\left({{l_i} - {q_i}} \right)}^2},}\\ {0,} \end{array}} \right.} \begin{array}{*{20}{c}} {{\rm{if}}{q_i} > {u_i},}\\ {{\rm{if}}{q_i} <{l_i},}\\ {{\rm{otherwise}}{\rm{.}}} \end{array}$ | (5) |
其中:qi为Q中的值,ui与li分别为U和L中的值。
ZHANG Y和GLASS J在LB-Keogh算法的基础上提出了LB-PAA算法[4]。LB-PAA下界算法采用点对累积近似(piecewise aggregate approximation,PAA)表示法[23],分别表示原始序列与上下边界曲线,求取相应的下界距离。LB-PAA算法降低了原始序列的维度,简化了相似性搜索的运算过程,同时也减弱了部分噪声对结果的影响。
采用LB-PAA下界算法简化了运算过程,降低了时间复杂度,但其运算量依然很大,无法满足人们以较小代价进行时间序列挖掘的要求。
1.2 Map/Reduce下的时间序列相似性搜索算法为解决时间序列相似性搜索中,时间复杂度大、运算效率低的问题,本研究将并行计算策略引入到时间序列处理中,提出一种基于MapReduce机制的时间序列子序列相似性搜索。
MapReduce机制分为Map和Reduce两个步骤。Map的工作是分解,把需要并行处理的数据拆分成大量数据片段,为分布式集群中的每一台计算机分配一个数据片段分别进行处理;而Reduce的工作与Map正好相反,负责将Map分开的数据在运算完成后再次整合到一起,并将最终汇总的结果输出[24, 25]。
采用基于MapReduce机制的并行方式进行运算,必须满足以下两个要求:任务能够等比例缩放,即当任务扩大或缩小时其单元任务不变,分配给每个节点的工作相同;要求所有任务完全独立,即任意两次运算之间没有必然关联,一次运算不以另一次运算为前提。
分析下界算法过滤与DTW距离计算的处理过程,其都以一条时间子序列为运算单元,且任务独立无关联,满足MapReduce并行计算的要求,因此可以在这两个阶段引入MapReduce策略进行并行处理。
1.2.1 LB-PAA下界算法的并行处理采用下界算法对时间序列进行过滤时,需要对每一条时间序列求解其相对参考序列的下界距离[26]。
(1)Map阶段
①通过DistributedCache类将查询序列T中的所有子序列Ci按照节点性能分配给各节点,并将参考序列Q及下界阈值d发送到各节点。
②对每一节点,使用公式(5)计算其分配到的子序列与参考序列的下界距离Dlb-PAA(C,Q),节点内串行运算。
③每一节点中比较所有子序列下界距离Dlb-PAA(Ci,Q)与阈值d的大小,将满足条件的子序列写入该节点对应矩阵Zi。
④将所有节点计算得到的Zi矩阵输出。
(2)Reduce阶段
①从Mapper处获得中间结果(即Zi矩阵)。
②汇总所有临时矩阵中的值,合并成最终结果矩阵Z。
③把最终矩阵Z(即候选集)输出给主函数。
1.2.2 DTW距离计算的并行处理由1.2.1中得到子序列候选集,分别构建其时间弯曲矩阵,计算每一条子序列与参考序列之间的DTW距离。
(1)Map阶段
①通过DistributedCache类将候选集Z中的所有序列zi按照节点性能分配给各节点,并将参考序列Q发送到各节点;
②在每一节点内,使用DTW距离计算公式计算得出所有序列与参考序列的DDTW(zi,Q),求出其中的最小值;
③将DTW距离最小的序列及其DTW距离输出。
(2)Reduce阶段
①从Mapper处获得中间结果;
②汇总所有Mapper的临时结果,求出其中的最小值;
③把最终结果(所有子序列中DTW距离最小,即相似度最高的序列,及其DTW距离)输出给主函数。
2 试验与分析本次并行试验的运行环境为Windows 7系统,8 G内存,Intel(R)Core(TM)i7-3770 CPU@3.40 GHz。
试验采用一组加利福尼亚大学机器学习实验室的ECG数据([20140000×1])及参考序列ecg-query([421×1])。该组数据跨度大,具有代表性,用于验证LB-Keogh、LB-PAA等算法。
本试验从ECG序列中随机选取部分子序列作为试验对象,并行计算从2个计算节点开始,逐个递增,以2为节点增长步长,直至8个节点。
试验主要从两个方面进行:MapReduce机制下进行PAA下界过滤和DTW距离计算的运算时间,以及并行加速比(单机运算时间与并行运算时间的比值)随节点数的变化情况。
2.1 试验一随机选取DTW序列中的102,103,104,105个子序列,使用LB-PAA算法和ecg-query序列进行下界过滤,在单机环境和MapReduce并行环境下进行运算。
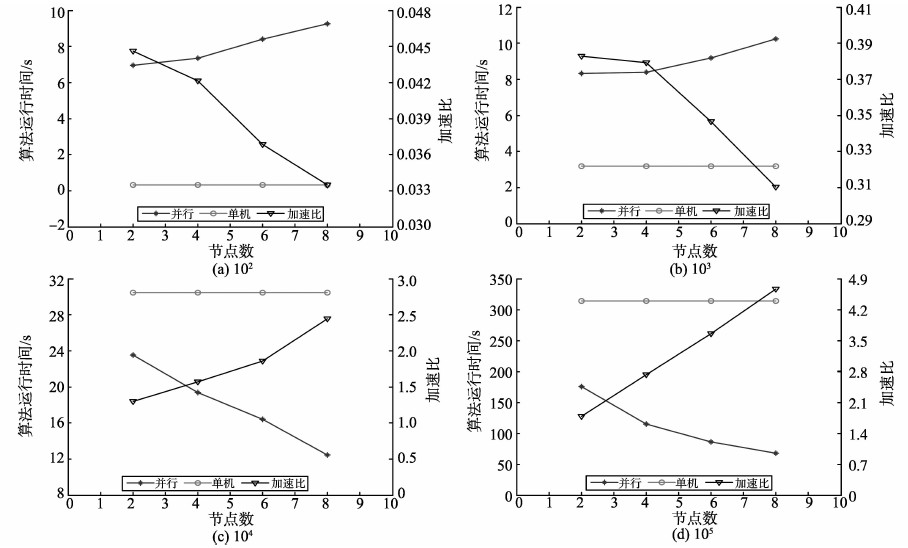
试验中LB-PAA算法以12作为弯曲半径,10作为段点数构造下界函数。试验结果如图 3所示。
|
图3 不同数量级下界过滤运算时间及加速比 Fig. 3 Calculating time and speedup rate of lower bound filter on different order of magnitudes |
由试验一可知,在使用LB-PAA算法进行下界过滤时,如果取102、103个子序列作为试验数据,如图 3(a)、(b)所示,并行运算所需的时间比单机运行多,且随节点数的增加而增加;而当取104、105个子序列作为试验数据时,如图 3(c)、(d)所示,并行运算需要的时间远少于单机运行,且随节点数的增加而减少。
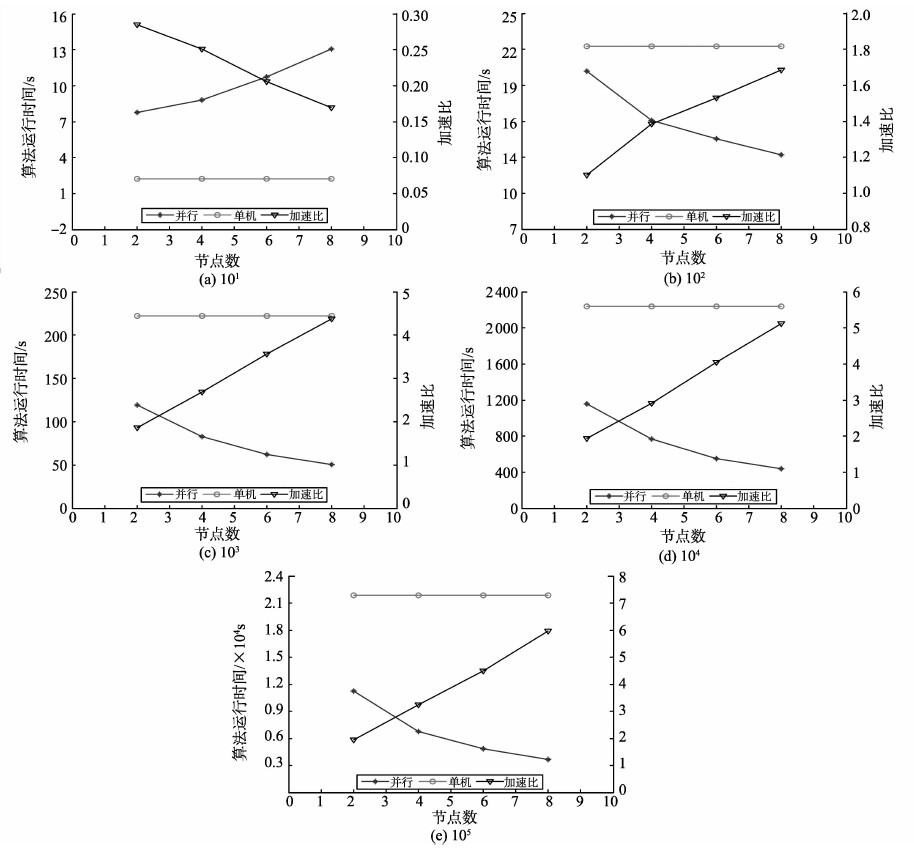
2.2 试验二随机选取DTW序列中的101,102,103,104,105个子序列构成的矩阵,使用DTW距离算法求矩阵中与ecg-query序列距离最小的子序列,分别在单机环境和MapReduce并行环境下进行运算,记录并分析其结果。计算过程中,选择12为弯曲半径构造弯曲路径的全局约束。试验结果如图 4所示。
|
图4 不同数量级DTW距离运算时间及加速比 Fig. 4 Calculating time and speedup rate of DTW distance on different order of magnitudes |
由试验二可知,在计算时间序列DTW距离时,如果取101个子序列作为实验数据,如图 4(a)所示,并行运算所需的时间比单机运行多,且随节点数的增加而增加;而当取102、103、104、105个子序列作为实验数据时,如图 4(b)、(c)、(d)、(e)所示,并行运算需要的时间远少于单机运行,且随节点数的增加而减少。
2.3 试验分析试验一中,取102个子序列作为试验数据,单机运行时间为0.31 s,而8节点运算时间为9.26 s。试验二中,取101个子序列作为试验数据,单机运行时间为2.21 s,而8节点运算时间为13.04 s。
由于MapReduce执行并行任务前需要进行初始化,不论是大规模运算还是小规模运算,都需要依次执行Map和Reduce两个基本步骤,而单机运行则较为灵活,在处理小规模运算时会消耗更少的时间,因此并行机制不适合处理小规模数据运算。
试验一中,取个子序列作为实验数据,单机运行时间为314.12 s,而8节点运算时间为67.42 s,加速约5倍。实验二中,取101个子序列作为实验数据,单机运行时间为21 863.21 s,而8节点运算时间为3 667.25 s,加速约6倍。
可见,当样本规模变大,并行计算的优势开始体现出来,并行运算时间比单机运算时间少。随着节点数的增多,并行运算消耗的时间不断减少,加速比不断变大。综上所述,当数据量较小时,MapReduce并行机制无法体现其优势,只有数据量达到一定规模,集群中所有节点同时工作时,才能显示出其远超单机运算的效率,大大减少运算时间。
3 结语本研究将时间序列的相似性搜索与MapReduce机制相结合,在并行环境下进行子序列相似性搜索,以较低的成本实现高速运算。试验结果表明,当数据规模较大时,本算法采用MapReduce并行机制有效降低了任务复杂度,提高了运算效率,减少了运算时间。由于数据的存取速度低于处理速度,会影响总体运算效率,为改善这一问题,在未来的工作中将对MapReduce算法的存取机制进行相关研究。
| [1] | BHADURI K, ZHU Q, OZA N C, et al. Fast and flexible multivariate time series subsequence search[C]//Proc of the 2010 IEEE Int l Conf on Data Mining. Sydney, Australia: IEEE, 2010:48-57.( 1) 1) |
| [2] | BERNDT D J, CLIFFORD J. Using dynamic time warping to find patterns in time series[C]//KDD Workshop. Seattle, USA:Springer US, 1994:359-370.( 1) 1) |
| [3] | KEOGH E, RATANAMAHATANA C A. Exact indexing of dynamic time warping[J]. Knowledge and Information Systems, 2005(7):358-386.( 2) 2) |
| [4] | ZHANG Y, GLASS J. A piecewise aggregate approximation lower-bound estimate for posteriorgram-based dynamic time warping[C]//Interspeech. Florence,Italy:IEEE, 2011:1909-1912.( 2) 2) |
| [5] | 丁静,杨善林,罗贺,等. 云计算环境下的数据挖掘服务模式[J]. 计算机科学, 2012, 39(6):217-219. DING Jing, YANG Shanlin, LUO He, et al. Data mining service model in cloud computing environment[J]. Computer Science, 2012, 39(6):217-219.(  1) 1) |
| [6] | 杨来,史忠植,梁帆,等. 基于Hadoop云平台的并行数据挖掘方法[J].系统仿真学报,2013,25(5):936-944. YANG Lai, SHI Zhongzhi, LIANG Fan, et al. Parallel approach in data mining based on hadoop cloud platform[J]. Journal of System Simulation, 2013, 25(5):936-944.(  1) 1) |
| [7] | 程苗. 基于云计算的Web数据挖掘[J]. 计算机科学,2011,38(10):146-149. CHENG Miao. Web data mining based on cloud computing[J]. Computer Science, 2011, 38(10):146-149.(  1) 1) |
| [8] | 陈光鹏,杨育彬,高阳,等. 一种基于Map/Reduce的频繁闭项集挖掘算法[J]. 模式识别与人工智能,2012,25(2):220-224. CHEN Guangpeng, YANG Yubin, GAO Yang, et al. Closed frequent itemset mining based on mapreduce[J]. PR&AI, 2015, 25(2):220-224.(  1) 1) |
| [9] | 田国会,许亚雄. 云机器人:概念、架构与关键技术研究综述[J]. 山东大学学报(工学版),2014,44(6):47-54. TIAN Guohui, XU Yaxiong. Cloud robotics: concept, architectures and key technologies[J]. Journal of Shandong University(Engineering Science), 2014, 44(6):47-54.(  1) 1) |
| [10] | ZHU Q, WANG X Y, KEOGH E, et al. An efficient and effective similarity measure to enable data mining of petroglyphs[J]. Data Mining and Knowledge Discovery, 2011, 23(1):91-127.( 1) 1) |
| [11] | PAPAPETROU P, ATHITSOS V, POTAMIAS M, et al. Embedding-based subsequence matching in time-series databases[J]. ACM Transactions on Database Systems, 2011, 36(3):17.( 1) 1) |
| [12] | 周大镯,吴晓丽,闫红灿. 一种高效的多变量时间序列相似查询算[J]. 计算机应用,2008,28(10):2541-2543. ZHOU Dazhuo, WU Xiaoli, YAN Hongcan. An efficient similarity search for multivariate time series[J]. Computer Applications, 2008, 28(10):2541-2543.(  1) 1) |
| [13] | FU AWC, KEOGH E, LAU LYH, et al. Scaling and time warping in time series querying[J]. The VLDB Journal, 2008, 17:899-921.( 1) 1) |
| [14] | MU B, YAN J L. Efficient time series lower bounding technique[J]. Computer Engineering and Applications, 2009, 45(11):168-171.( 1) 1) |
| [15] | BEGUM N,KEOGH E. Rare time series motif discovery from unbounded streams[J]. Proceedings of the VLDB Endowment, 2014, 8(2):149-160.( 1) 1) |
| [16] | ZHOU D Z, JIANG W B, LI M Q. Efficient clustering algorithm for multivariate time series[J]. Computer Engineering and Applications, 2010, 46(1):137-139.( 1) 1) |
| [17] | THANAWIN Rakthanmanon, BILSON Campana, ABDULLAH Mueen, et al. Searching and mining trillions of time series subsequences under dynamic time warping[C]//KDD′12-18th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York, USA:IEEE, 2012:262-270.( 1) 1) |
| [18] | WANG X, MUEEN A, DING H, et al. Experimental comparison of representation methods and distance measures foe time series data[J]. Data Mining and Knowledge Discovery, 2013, 26(2):275-309.( 1) 1) |
| [19] | SHOKOOHI-YEKTA M, WANG J, KEOGH E. On the non-trivial generalization of dynamic time warping to the multi-dimensional case[C]//SDM Vancouver,Canada:Society for Industrial and Applied Mathematics, 2015:289-297.( 1) 1) |
| [20] | SAKURAI Y, YOSHIKAWA M, FALOUTSOS C. FTW: fast similarity search under the time warping distance[C]//PODS. Baltimore, Maryland:Sprinter US, 2005:326-337.( 1) 1) |
| [21] | BANK Z, ABONYI J. Correlation based dynamic time warping of multivariate time series[J]. Expert Systems with Applications, 2012, 39(17):12814-12823.( 1) 1) |
| [22] | 李正欣,张凤鸣,李克武,等.一种支持DTW距离的多元时间序列索引结构[J]. 软件学报,2014,25(3):560-575. LI Zhengxin, ZHANG Fengming, LI Kewu, et al. Index structure for multivariate time series under DTW distance metric[J]. Journal of Software, 2014, 25(3):560-575.(  1) 1) |
| [23] | HYUNJIN Yoon, KIYOUNG Yang, CYRUS Shahabi. Feature subset selection and feature ranking for multivariate time series[J]. IEEE Transactions on Knowledge and Data Engineering, 2005, 17(9):1186-1198.( 1) 1) |
| [24] | 李伟卫,赵航,张阳,等. 基于MapReduce的海量数据挖掘技术研究[J].计算机工程与应用,2013,49(20):112-117. LI Weiwei, ZHAO Hang, ZHANG Yang, et al. Research on massive data mining based on mapreduce[J]. Computer Engineering and Applications, 2013, 49(20):112-117.(  1) 1) |
| [25] | 何东之,张吉沣,赵鹏飞. 不确定传播算法的MapReduce并行化实现[J]. 山东大学学报(工学版),2015,44(5):22-28. HE Dongzhi, ZHANG Jifeng, ZHAO Pengfei. Parallel implementing probabilistic spreading algorithm using MapReduce programming mode[J]. Journal of Shandong University(Engineering Science), 2015, 44(5):22-28.(  1) 1) |
| [26] | AGRAWAL R, FALOUTSOS C, SWAMI A. Efficient similarity search in sequence databases[C]//Proc of the 4th Int′l Conf on Foundations of Data Organization and Algorithms. Chicoga, USA:Springer Berlin Heidelberg, 1993:69-84.( 1) 1) |



