2. 山东省分布式计算机软件新技术重点实验室, 山东 济南 250014
2. Shandong Provincial Key Laboratory for Novel Distributed Computer Software Technology, Jinan 250014, Shandong, China
随着网络和存储技术的不断发展,高维数据的数量迅速增加,给数据分析带来了挑战。如何保持数据结构不变,通过降维处理,把高维数据投影到低维空间,成为近年研究热点问题[1, 2, 3, 4, 5, 6]。面向不同应用,学者们相继提出多种降维技术。目前流行的降维算法有主成分分析(principal component analysis,PCA)[7,8]、线性判别分析(linear discriminant analysis,LDA)[9]、局部保持投影(locality preserving projection,LPP)[10,11]、局部线性嵌入(locally linear embedding,LLE)[12]、邻域保持嵌入(neighborhood preserving embedding,NPE)[13]等。其中NPE是一种无监督的基于局部的线性降维算法,作为一种保持数据局部邻域不变的子空间学习算法,在流形学习上具有很好的性能,广泛应用于人脸识别[14]。但是由于NPE没有利用数据的类别信息,且基于局部,在面向分类的应用中性能不高。对此,判别邻域嵌入(discriminant neighborhood embedding,DNE)[15]、判别稀疏邻域保持嵌入(discriminant sparse neighbourhood preserving embedding,DSNPE)[16]、稀疏邻域保持嵌入(sparse neighbourhood preserving embedding,SNPE)[17,18,19]相继被提出。
本研究提出一种基于全局距离和类别信息的邻域保持嵌入算法。在传统NPE算法构造邻域图选取邻近点的欧氏距离公式中,加入了表征全局距离的全局因子和表示类别信息的函数项。全局因子对样本点间的距离进行全局约束,使分布不均匀的样本变得平滑均匀。表示类别信息的函数项使类内距离减小,类间距离增大。通过优化邻域,使降维后的数据具有更好的可分性。
1 NPE算法作为一种保持数据局部流形结构的线性降维算法,NPE的主要思想是保持子流形下数据局部几何结构不变,得到原始数据的子空间描述,即找到能够最好保持原始数据局部邻域结构的低维嵌入[20]。现给定训练样本Xm×n=[x1,x2,…,xn],其中xi∈Rm,n为训练样本个数,m为训练样本维数。NPE旨在找到一个最优转换矩阵A=[a1,a2,…,ad],把n个样本点通过转换矩阵A投影至低维空间Rd(d <<m)。在低维空间Rd中,样本点xi表示为yi,即yi=AT
(1)构造邻接图G
G为n个样本点构成的图,如果两个样本点xi和xj是近邻,则用边将其连接,否则不连接。判断两点是否为近邻有两种方法,一种是KNN方法,另一种是ε-邻域方法,两种方法均是基于传统欧氏距离。
(2)计算权值矩阵W
根据邻接图G,每个样本点由其邻近点的线性组合表示。如果到xj间没有边,则Wij=0;否则Wij通过最小化以下代价函数来度量:
| $\min \sum\limits_i {||{x_i}} - \sum\limits_j {{W_{ij}}} {x_j}|{|^2},\sum\limits_j {{W_{ij}}}=1\;.$ | (1) |
(3)计算投影矩阵A
通过Wij在低维空间Rd重构对应的点yi。即最小化以下代价函数:
| $\min \sum\limits_i {||{y_i}} - \sum\limits_j {{W_{ij}}} {y_j}|{|^2}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{=}}\;{\rm{min}}\;{A^T}XM{X^T}A\;,$ | (2) |
其中,M=(I-W)T(I-W)是对称半正定矩阵;I是单位矩阵。转换矩阵A的列向量通过求解以下广义特征值的特征向量得到:
| $XM{X^T}a=\lambda X{X^{\rm{T}}}a,$ | (3) |
得到转换矩阵A=[a1,a2,…,ad],通过Y=ATX得到X在低维空间Rd的低维表示。
2 基于全局距离和类别信息的邻域保持嵌入算法NPE是一种基于局部的线性降维算法,通过选取样本点的邻近点构造权值矩阵进行投影,这种基于局部的方法往往忽略了样本点与非邻近点之间的关系。对于分布不均匀的样本,距离较远的两个样本点,其相对距离不一定远。比如两个样本点xi和xj,xi与其他样本点距离都很近,xj与其他样本点距离都很远,而xi是xj的最近邻点,通过传统NPE构造邻域图的距离公式计算的话,xi是xj的邻近点,而xj并不是xi的一个邻近点,忽略了xj对xi的影响。通过这种方法选取邻近点面对分布不均匀的样本存在一定的局限性,不能准确找到近邻。基于全局的方法不仅考虑到样本点与邻近点之间的关系,同样考虑到样本点与非邻近点之间的关系。
针对NPE算法基于局部的局限性,本研究在保持数据局部几何结构的前提下,对选取邻近点的距离公式进行了改进,提出基于全局距离和类别信息的邻域保持嵌入算法(neighborhood preserving embedding algorithm based on global distance and label information,GLI-NPE)。在NPE通过KNN构造邻域图的欧氏距离公式中,加入了表征全局距离的全局因子对其进行距离约束,缩短分布稀疏样本点之间的相对距离,使分布不均匀的样本点变得平滑均匀。对欧氏距离进行距离约束的公式如下:
| ${d_{ij}}=\frac{{||{x_i} - {x_j}||}}{{\sqrt {{D_i}{D_j}} }}\;,$ | (4) |
其中:‖xi-xj‖表示xi和xj之间的欧氏距离,$\sqrt {{D_i}{D_j}} $是对xi和xj进行距离约束的全局因子,Di和Dj分别表示xi和xj与所有点的平均距离。通过全局因子对xi和xj两点进行距离约束,用相对距离代替普通欧式距离,充分考虑样本点与非邻近点之间的关系,使分布不均匀的样本变得平滑均匀。
另外,本研究针对无监督NPE算法在面向分类应用的局限性进行了改进。将数据类别信息作为影响参数加入到计算近邻的距离公式中,旨在使类内样本点紧凑,类间样本点疏离,提高所选邻近点的质量。表示类别信息的影响参数如下:
| $\delta({x_i},{x_j})=\left\{ \begin{array}{l} \gamma \;\;\;\;\;\;\;\;\;\;\;{x_i}{\rm{和}}{x_j}{\rm{同类}}\\ \frac{1}{\gamma }\;\;\;\;\;\;\;\;\;\;{x_i}{\rm{和}}{x_j}{\rm{不同类}} \end{array} \right.{\rm{ }},$ | (5) |
其中:γ为(0,1)的常数。将公式(4)和公式(5)结合,改进的距离公式如下:
| ${d_{ij}}=\frac{{||{x_i} - {x_j}||}}{{\sqrt {{D_i}{D_j}} }}\delta({x_i},{x_j})\;.$ | (6) |
当xi和xj同类时,δ(xi,xj)为(0,1)之间的常数,dij减小;当xi和xj不同类时,δ(xi,xj)为大于1的常数,dij增大。从而使类内紧凑,类间疏离。改进的GLI-NPE算法具体步骤如下:
(1)通过距离公式(6)选取K个邻近点,构造邻域图。
(2)与NPE算法的第2步相同,对构造的邻域图计算重构权值矩阵W。
(3)与NPE算法的第3步相同,利用M=(I-W)T(I-W)构造矩阵M,通过公式(3)计算M的特征值和特征向量,得到投影矩阵A,通过Y=ATX,得到样本X在低维空间的表示Y。
全局因子对两点距离进行全局约束,在相对距离下选取邻近点,提高对分布不均匀样本的鲁棒性。类别信息使样本点类内紧凑类间疏离,选取相似性更大的邻近点。综合两点,使降维后的数据可分性更强,从而提高分类性能。
3 试验结果与分析为验证GLI-NPE算法的有效性,本研究选取UCI机器学习数据库的5个标准数据集和3个人脸数据集作为试验数据对象,在MATLAB环境下与PCA、LPP、LDA、LLE、DNE、NPE进行对比试验。本试验统一采用最近邻分类器对降维后的数据进行分类,取12个近邻,γ取0.6。
首先对数据集进行处理,采用较常用的精度测试方法10倍交叉验证进行试验。即将数据集分成10组,每次选择其中1组作为测试数据,剩余9组作为训练数据,试验可以重复10次。
3.1 基于UCI数据集的试验为验证算法的有效性,本研究从UCI数据集上选择了5个数据集,其信息描述见表 1。
| 表1 UCI中5个数据集的描述信息 Table 1 Description of 5 data sets in UCI |
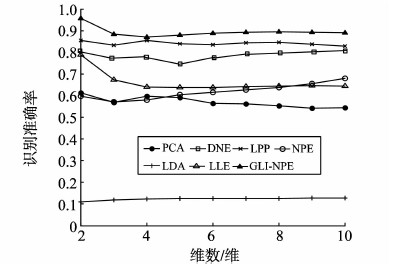
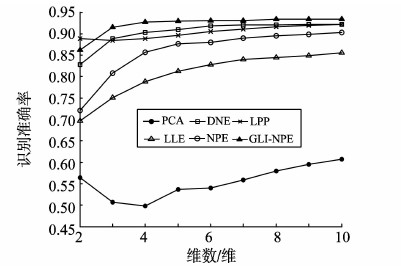
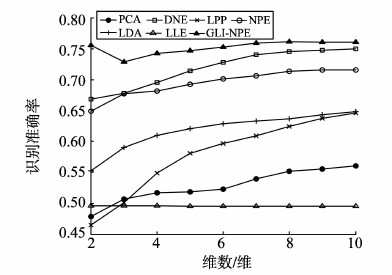
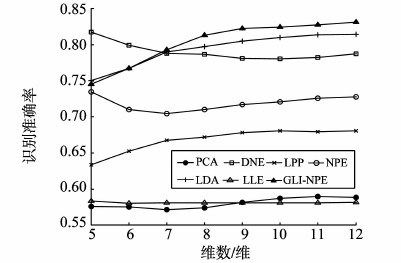
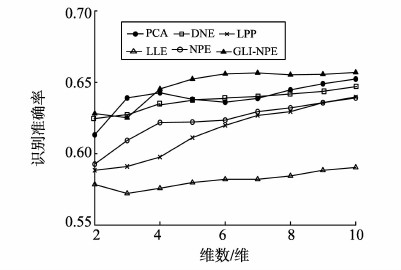
图 1~5是UCI中5个不同子数据集的试验结果,表示不同特征维数下算法的识别准确率,其中横轴为所降到的维数,纵轴为最终分类结果的准确率。图 1为zoo数据集,识别率最高的是GLI-NPE,其次是LPP和DNE。图 2为wine数据集,GLI-NPE识别率最高,其次是LPP和DNE。图 3为heart数据集,GLI-NPE识别率最高,其次是DNE和NPE。图 4为sonar数据集,GLI-NPE识别率最高,其次是LDA和DNE。图 5为german数据集,GLI-NPE识别率最高,其次是PCA和NPE。
|
图1 zoo数据集 Fig. 1 zoo data set |
|
图2 wine数据集 Fig. 2 wine data set |
|
图3 heart数据集 Fig. 3 heart data set |
|
图4 sonar数据集 Fig. 4 sonar data set |
|
图5 german数据集 Fig. 5 german data set |
试验结果表明,本文提出的GLI-NPE方法的识别率明显高于PCA、LPP、LDA、LLE、DNE、NPE。因为其考虑了数据的类别信息,使样本点类内紧凑类间疏离,优化选择邻近点,提高分类性能。同时与其他方法相比,GLI-NPE的稳定性较高,这是因为其同时考虑了全局距离,通过加入对全局距离约束的全局因子,增大了对不均匀样本的鲁棒性,因此其分类性能也更加稳定。DNE同样考虑了数据的类别信息,是有监督的学习方法,因此识别率也较高。但是GLI-NPE的稳定性要高于DNE,因为GLI-NPE不只考虑了类别信息,同时考虑了全局距离,增大了对样本的鲁棒性。从试验结果可看出,当所降维数过于低时,这些方法的识别率大都较低。这是因为所降维数越多,降维过程中损失的原始信息也会越大。因此,在降维处理中,选择恰当的维数也是问题的关键。
3.2 基于人脸数据集的试验为验证GLI-NPE在人脸数据集上的有效性,选择了3个著名的人脸数据集进行试验,分别是ORL[21]、Yale、Extended Yale B[22]。本研究统一将图像调整为32×32像素。对于ORL和Yale数据集,由于其数据维数大于样本数,因此先采用PCA对其进行基础降维,再用PCA、LPP、LDA、LLE、NPE、GLI-NPE进行二次降维,然后利用最近邻分类器进行识别,对比分类结果。其信息描述如表 2所示。
| 表2 3个人脸图像数据集的描述 Table 2 Description of 3 face image data sets |
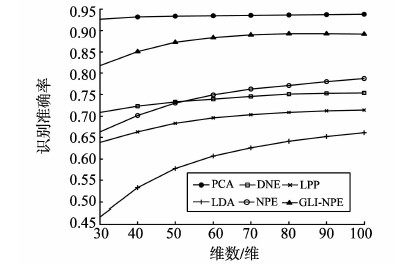
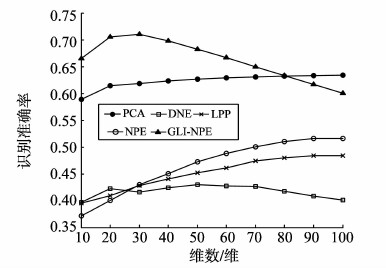
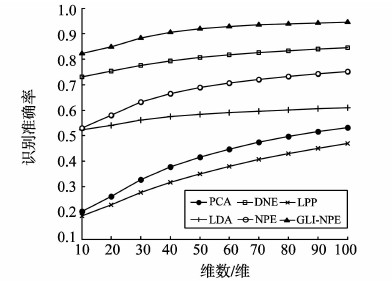
图 6是在ORL数据集上的试验结果,PCA识别率最高,其次是GLI-NPE。图 7是在Yale数据集上的试验结果,GLI-NPE识别率最高,其次是PCA。图 8是在Yale B数据集的试验结果,GLI-NPE识别率最高,其次是DNE。
|
图6 ORL数据集 Fig. 6 ORL data set |
|
图7 Yale数据集 Fig. 7 Yale data set |
|
图8 Yale B数据集 Fig. 8 YaleB data set |
试验结果表明,GLI-NPE在Yale数据集和Yale B数据集识别率都是最高的。3个数据集上GLI-NPE的识别率明显高于NPE和DNE,且性能稳定。这是因为GLI-NPE不仅考虑了类别信息使类内紧凑、类间疏离,选择相似性更高的邻近点,同时对数据进行全局约束从而提高对样本点的鲁棒性。其中通过保持图像空间全局结构信息的PCA,在数据集ORL上也有较高的识别率。ORL数据集和YaleB数据集上可以看出,当所降维数过低时,损失的原始信息过多,这些方法的识别率也都较低。
4 结论本研究提出一种基于全局距离和类别信息的邻域保持嵌入算法(GLI-NPE),该算法在NPE利用KNN传统欧氏距离计算邻域点的距离公式中,加入了表征全局距离的全局因子和表示类别信息的函数项。全局因子对数据样本点之间的距离进行全局距离约束,提高对分布不均匀样本的鲁棒性。类别信息使类内距离减小、类间距离增大,从而使找到的样本点相似性更大。通过邻域优化,使降维后的数据具有更好的可分性,从而提高分类性能。为了验证该算法的分类性能,将GLI-NPE与PCA、LPP、LDA、LLE、DNE、NPE多种降维方法进行了比较,试验结果表明该算法对数据具有很好的分类性能。下一步我们将从如何更好的表示数据类别信息角度进行更深入的研究。
| [1] | 周志华, 杨强. 机器学习及其应用[M].北京:清华大学出版社, 2011:87-95.( 1) 1) |
| [2] | EGECIOGLU O, FERHATOAMANOGLU H, OGRAS U. Dimensionality reduction and similarity computation by inner-product approximations[J].IEEE Transactions on Knowledge and Data Engineering, 2004, 16(6):714-726.( 1) 1) |
| [3] | BELKIN M, NIYOGI P. Laplacian eigenmaps for dimensionality reduction and data representation[J]. Neural Computation, 2003, 15(6):1373-1396.( 1) 1) |
| [4] | 赵连伟, 罗四维, 赵艳敞, 等. 高维数据流形的低维嵌入及嵌入维数研究[J]. 软件学报, 2005, 16(8):1423-1430. ZHAO Lianwei, LUO Siwei, ZHAO Yanchang, et al. Study on the low-dimensional embedding and the embedding dimensionality of manifold of high-dimensional data[J].Journal of Software, 2005, 16(8):1423-1430.(  1) 1) |
| [5] | TENENBAUMe J B, DE SILVA V, LANGFORD J C. A global geometric framework for nonlinear dimensionality reduction[J].Science, 2000, 290(5500):2319-2323.( 1) 1) |
| [6] | HUANG Hong, HUANG Yunbiao. Improved discriminant sparsity neighborhood preserving embedding for hyperspectral image classification[J].Neurocomputing, 2014, 136(2014):224-234.( 1) 1) |
| [7] | JOLLIFFE I T. Principle component analysis[M]. Berlin: Springer-Verlag, 1986: 384-389.( 1) 1) |
| [8] | WANG Fei, WANG Xin, ZHANG Daoqiang, et al. MarginFace: A novel face recognition method by average neighborhood margin maximization[J]. Pattern Recognition, 2009, 42(11):2863-2875.( 1) 1) |
| [9] | BELHUMEUR P N, HESPANDA J P, KRIEGMAN D J. Eigenfaces vs. fisherfaces: Recognition using class specific linear projection[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1997, 19(7):711-720.( 1) 1) |
| [10] | HE Xiaofei, NIYOGI P. Locality preserving projections[J]. Advances in Neural Information Processing Systems, 2005, 45(1):186-197.( 1) 1) |
| [11] | HAM J, LEE D D, SAUL L K. Semi-supervised alignment of manifolds[J]. International Workshop on Articial Intelligence & Statistics, 2005:120-127.( 1) 1) |
| [12] | ROWEIS S T, SAUL L K. Nonlinear dimensionality reduction by locally linear embedding[J]. Science, 2000, 290(5500):2323-2326.( 1) 1) |
| [13] | HE Xiaofei, CAI Deng, YAN Shuicheng, et al. Neighborhood preserving embedding[C]//Proceedings of the Tenth IEEE International Conference on Computer Vision Workshops. New York, USA: IEEE, 2005:1208-1213.( 1) 1) |
| [14] | YIN Fei, JIAO L C, SHANG Fanhua, et al. Sparse regularization discriminant analysis for face recognition[J]. Neurocomputing, 2014, 128:341-362.( 1) 1) |
| [15] | ZHANG Wei, XUE Xiangyang, LU Hong, et al. Discriminant neighborhood embedding for classification[J]. Pattern Recognition, 2006, 39(11):2240-2243.( 1) 1) |
| [16] | GUI Jie, SUN Zhenan, JIA Wei, et al. Discriminant sparse neighborhood preserving embedding for face recognition[J]. Pattern Recognition, 2012, 45(8):2884-2893.( 1) 1) |
| [17] | CHENG Bin, YANG Jianchao, YAN Shuicheng, et al. Learning with l1-graph for image analysis[J]. IEEE Transactions on Image Processing, 2010, 19(4):858-866.( 1) 1) |
| [18] | QIAO Lishan, CHEN Songcan, TAN Xiaoyan. Sparsity preserving projections with applications to face recognition[J]. Pattern Recognition, 2010, 43(1):331-341.( 1) 1) |
| [19] | 包兴, 张莉, 赵梦梦, 等. 基于类别信息的邻域保持嵌入算法[J]. 计算机科学, 2015, 42(5):94-97. BAO Xing, ZHANG Li, ZHAO Mengmeng, et al. Label information-based neighbourhood preserving embedding[J]. Computer Science, 2015, 42(5):94-97.(  1) 1) |
| [20] | WANG Yong, WU Yi. Complete neighborhood preserving embedding for face recognition[J]. Pattern Recognition, 2010, 43(3):1008-1015.( 1) 1) |
| [21] | SAMARIA F S, HARTER A C. Parameterisation of a stochastic model for human face identification[C]//Proceedings of the Second IEEE Workshop on Applications of Computer Vision. New York, USA: IEEE, 1994:138-142.( 1) 1) |
| [22] | LEE K C, HO J, KRIEGMAN D J. Acquiring linear subspaces for face recognition under variable lighting[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2005, 27(5):684-698.( 1) 1) |




